
【题目】已知函数f(x)=x2+ ![]() +alnx.
+alnx.
(Ⅰ)若f(x)在区间[2,3]上单调递增,求实数a的取值范围;
(Ⅱ)设f(x)的导函数f′(x)的图象为曲线C,曲线C上的不同两点A(x1 , y1)、B(x2 , y2)所在直线的斜率为k,求证:当a≤4时,|k|>1.
【答案】解:(Ⅰ)由 ![]() ,得
,得 ![]() .
.
因为f(x)在区间[2,3]上单调递增,
所以 ![]() ≥0在[2,3]上恒成立,
≥0在[2,3]上恒成立,
即 ![]() 在[2,3]上恒成立,
在[2,3]上恒成立,
设 ![]() ,则
,则 ![]() ,
,
所以g(x)在[2,3]上单调递减,
故g(x)max=g(2)=﹣7,
所以a≥﹣7;
(Ⅱ)对于任意两个不相等的正数x1、x2有
![]() >
> ![]()
= ![]()
![]()
= ![]() ,
,
∴ ![]() ,
,
而 ![]() ,
,
∴ ![]() =
= ![]()
= ![]() >
> ![]() ,
,
故: ![]() >
> ![]() ,即
,即 ![]() >1,
>1,
∴当a≤4时, ![]() .
.
【解析】(Ⅰ)将函数f(x)在区间[2,3]上单调递增,转化为导数函数f'(x)≥0在区间[2,3]上恒成立,从而求得a的取值范围;(Ⅱ)先利用基本不等式求得解题过程中的的关键不等式的取值范围,最后利用斜率公式列出不等式,从而证明当a≤4时,|k|>1.
【考点精析】本题主要考查了利用导数研究函数的单调性和基本不等式的相关知识点,需要掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;基本不等式:
在这个区间单调递减;基本不等式:![]()
![]() ,(当且仅当
,(当且仅当![]() 时取到等号);变形公式:
时取到等号);变形公式:![]()
![]() 才能正确解答此题.
才能正确解答此题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2x﹣3x2 , 设数列{an}满足:a1= ![]() ,an+1=f(an)
,an+1=f(an)
(1)求证:对任意的n∈N* , 都有0<an< ![]() ;
;
(2)求证: ![]() +
+ ![]() +…+
+…+ ![]() ≥4n+1﹣4.
≥4n+1﹣4.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)的导函数为f'(x),且满足 ![]() ,f(1)=e,则x>0时,f(x)( )
,f(1)=e,则x>0时,f(x)( )
A.有极大值,无极小值
B.有极小值,无极大值
C.既有极大值又有极小值
D.既无极大值也无极小值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ﹣2alnx+(a﹣2)x,a∈R.
﹣2alnx+(a﹣2)x,a∈R.
(1)当a=﹣1时,求函数f(x)的极值;
(2)当a<0时,讨论函数f(x)单调性;
(3)是否存在实数a,对任意的m,n∈(0,+∞),且m≠n,有 ![]() >a恒成立?若存在,求出a的取值范围;若不存在,说明理由.
>a恒成立?若存在,求出a的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,圆O是一半径为10米的圆形草坪,为了满足周边市民跳广场舞的需要,现规划在草坪上建一个广场,广场形状如图中虚线部分所示的曲边四边形,其中A,B两点在⊙O上,A,B,C,D恰是一个正方形的四个顶点.根据规划要求,在A,B,C,D四点处安装四盏照明设备,从圆心O点出发,在地下铺设4条到A,B,C,D四点线路OA,OB,OC,OD.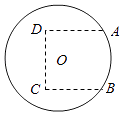
(1)若正方形边长为10米,求广场的面积;
(2)求铺设的4条线路OA,OB,OC,OD总长度的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代的数学名著,体现了古代劳动人民的数学智慧,其中第六章“均输”中,有一竹节容量问题,某人根据这一思想,设计了如图所示的程序框图,若输出m的值为35,则输入的a的值为 . 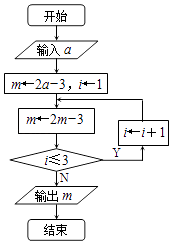
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P﹣ABC中,已知平面PBC⊥平面ABC.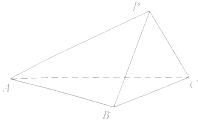
(1)若AB⊥BC,CP⊥PB,求证:CP⊥PA:
(2)若过点A作直线l⊥平面ABC,求证:l∥平面PBC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点(2,3)在椭圆 ![]() 上,设A,B,C分别为椭圆的左顶点、上顶点、下顶点,且点C到直线AB的距离为
上,设A,B,C分别为椭圆的左顶点、上顶点、下顶点,且点C到直线AB的距离为 ![]() .
.
(I)求椭圆C的方程;
(II)设M(x1 , y1),N(x2 , y2)(x1≠x2)为椭圆上的两点,且满足 ![]()
![]() =
= ![]() ,求证:△MON的面积为定值,并求出这个定值.
,求证:△MON的面积为定值,并求出这个定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com