
【题目】某商场准备在今年的“五一假”期间对顾客举行抽奖活动,举办方设置了![]() 两种抽奖方案,方案
两种抽奖方案,方案![]() 的中奖率为
的中奖率为![]() ,中奖可以获得
,中奖可以获得![]() 分;方案
分;方案![]() 的中奖率为
的中奖率为![]() ,中奖可以获得
,中奖可以获得![]() 分;未中奖则不得分,每人有且只有一次抽奖机会,每次抽奖中奖与否互不影响,并凭分数兑换奖品,
分;未中奖则不得分,每人有且只有一次抽奖机会,每次抽奖中奖与否互不影响,并凭分数兑换奖品,
(1)若顾客甲选择方案![]() 抽奖,顾客乙选择方案
抽奖,顾客乙选择方案![]() 抽奖,记他们的累计得分为
抽奖,记他们的累计得分为![]() ,若
,若![]() 的概率为
的概率为![]() ,求
,求![]()
(2)若顾客甲、顾客乙两人都选择方案![]() 或都选择方案
或都选择方案![]() 进行抽奖,问:他们选择何种方案抽奖,累计得分的均值较大?
进行抽奖,问:他们选择何种方案抽奖,累计得分的均值较大?
【答案】(1)![]() (2)当
(2)当![]() 时,他们都选择
时,他们都选择![]() 方案进行抽奖时,累计得分的均值较大;当
方案进行抽奖时,累计得分的均值较大;当![]() 时,他们都选择
时,他们都选择![]() 方案进行抽奖时,累计得分的均值较大;当
方案进行抽奖时,累计得分的均值较大;当![]() 时,他们都选择
时,他们都选择![]() 方案或都选择
方案或都选择![]() 方案进行抽奖时,累计得分的均值相等
方案进行抽奖时,累计得分的均值相等
【解析】
(1)首先求解出对立事件“![]() ”的概率,再根据对立事件概率公式求得结果;(2)利用二项分布均值公式求解出
”的概率,再根据对立事件概率公式求得结果;(2)利用二项分布均值公式求解出![]() 和
和![]() ,根据均值的性质求得两人全选
,根据均值的性质求得两人全选![]() 方案或
方案或![]() 方案的均值,比较两个均值的大小,得到
方案的均值,比较两个均值的大小,得到![]() 不同取值的情况下应选取的方案.
不同取值的情况下应选取的方案.
(1)由已知得,甲中奖的概率为![]() ,乙中奖的概率为
,乙中奖的概率为![]() ,且两人中奖与否互不影响
,且两人中奖与否互不影响
记“这![]() 人的累计得分
人的累计得分![]() ”的事件为
”的事件为![]() ,则事件
,则事件![]() 的对立事件为“
的对立事件为“![]() ”
”
![]()
![]()
![]()
(2)设甲、乙都选择![]() 方案抽奖的中奖次数为
方案抽奖的中奖次数为![]() ,都选择
,都选择![]() 方案抽奖的中奖次数为
方案抽奖的中奖次数为![]()
则这两人选择![]() 方案抽奖累计得分的均值为
方案抽奖累计得分的均值为![]() ,选择
,选择![]() 方案抽奖累计得分的均值为
方案抽奖累计得分的均值为![]()
由已知可得:![]() ,
,![]()
![]() ,
,![]()
![]() ,
,![]()
若![]() ,则
,则![]()
![]()
若![]() ,则
,则![]()
![]()
若![]() ,则
,则![]()
![]()
综上所述:当![]() 时,他们都选择
时,他们都选择![]() 方案进行抽奖时,累计得分的均值较大
方案进行抽奖时,累计得分的均值较大
当![]() 时,他们都选择
时,他们都选择![]() 方案进行抽奖时,累计得分的均值较大
方案进行抽奖时,累计得分的均值较大
当![]() 时,他们都选择
时,他们都选择![]() 方案或都选择
方案或都选择![]() 方案进行抽奖时,累计得分的均值相等
方案进行抽奖时,累计得分的均值相等


 学业测评一课一测系列答案
学业测评一课一测系列答案科目:高中数学 来源: 题型:
【题目】设a,b,c分别是![]() 的三条边,且
的三条边,且![]() .我们知道,如果
.我们知道,如果![]() 为直角三角形,那么
为直角三角形,那么![]() (勾股定理).反过来,如果
(勾股定理).反过来,如果![]() ,那么
,那么![]() 为直角三角形(勾股定理的逆定理).由此可知,
为直角三角形(勾股定理的逆定理).由此可知,![]() 为直角三角形的充要条件是
为直角三角形的充要条件是![]() .请利用边长a,b,c分别给出
.请利用边长a,b,c分别给出![]() 为锐角三角形和钝角三角形的一个充要条件,并证明.
为锐角三角形和钝角三角形的一个充要条件,并证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2sin2(x+![]() )-2
)-2![]() cos(x-
cos(x-![]() )-5a+2.
)-5a+2.
(1)设t=sinx+cosx,将函数f(x)表示为关于t的函数g(t),求g(t)的解析式;
(2)对任意x∈[0,![]() ],不等式f(x)≥6-2a恒成立,求a的取值范围.
],不等式f(x)≥6-2a恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]()
(![]() )求数列
)求数列![]() 的通项公式;
的通项公式;
(![]() )若数列
)若数列![]() 满足
满足![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(![]() )在(
)在(![]() )的条件下,设
)的条件下,设![]() ,问是否存在实数
,问是否存在实数![]() 使得数列
使得数列![]() 是单调递增数列?若存在,求出
是单调递增数列?若存在,求出![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了如图所示的折线图.根据该折线图,下列结论错误的是( )
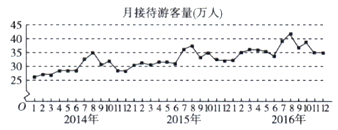
A.月接待游客量逐月增加
B.年接待游客量逐年增加
C.各年的月接待游客量高峰期大致在7,8月
D.各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com