
【题目】已知![]() 为棱长
为棱长![]() 的正方体,
的正方体, ![]() 为棱
为棱![]() 的中点.
的中点.
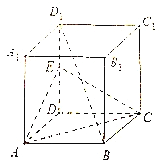
(1)求三棱锥![]() 的体积;
的体积;
(2)求证: ![]() 平面
平面![]() .
.
【答案】(1)![]() ;(2)见解析.
;(2)见解析.
【解析】试题分析:(1)高为ED,再根据锥体体积公式计算体积(2)连接![]() 交
交![]() 于点
于点![]() ,根据三角形中位线性质得
,根据三角形中位线性质得![]() ,再根据线面平行判定定理得结论
,再根据线面平行判定定理得结论
试题解析:(1)体积![]()
![]()
(2)连接![]() 交
交![]() 于点
于点![]() ,则
,则![]() 为
为![]() 的中位线,即
的中位线,即![]() ,
,
又![]() 面
面![]() ,
, ![]() 面
面![]() ,得到
,得到![]()
![]() 平面
平面![]() .
.
【题型】解答题
【结束】
18
【题目】已知抛物线![]() :
: ![]() 的焦点
的焦点![]() 为圆
为圆![]() 的圆心.
的圆心.
(1)求抛物线![]() 的标准方程;
的标准方程;
(2)若斜率![]() 的直线
的直线![]() 过抛物线的焦点
过抛物线的焦点![]() 与抛物线相交于
与抛物线相交于![]() 两点,求弦长
两点,求弦长![]() .
.
科目:高中数学 来源: 题型:
【题目】若f(x)是定义在(0,+∞)上的增函数,且对一切x,y>0,满足![]() .
.
(1)求f(1)的值;
(2)若f(6)=1,解不等式f(x+3)-f(![]() )<2.
)<2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,a,b,c分别是三内角A,B,C所对应的三边,已知b2+c2=a2+bc
(1)求角A的大小;
(2)若 ![]() ,试判断△ABC的形状.
,试判断△ABC的形状.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(选修4﹣4:坐标系与参数方程)
已知曲线C1的参数方程为 ![]() (t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=2sinθ.
(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=2sinθ.
(1)把C1的参数方程化为极坐标方程;
(2)求C1与C2交点的极坐标(ρ≥0,0≤θ<2π)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本题满分12分)
一个盒子中装有4张卡片,每张卡片上写有1个数字,数字分别是1、2、3、4,现从盒子中随机抽取卡片.
(Ⅰ)若一次从中随机抽取3张卡片,求3张卡片上数字之和大于或等于7的概率;
(Ⅱ)若第一次随机抽取1张卡片,放回后再随机抽取1张卡片,求两次抽取的卡片中至少一次抽到数字2的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() .
.
(1)求函数![]() 的解析式;
的解析式;
(2)求函数![]() 的单调区间和极值.
的单调区间和极值.
【答案】(1)![]() ;(2)见解析.
;(2)见解析.
【解析】试题分析:(1)根据导数几何意义得![]() ,再与
,再与![]() 联立方程组解得
联立方程组解得![]() ,
, ![]() (2)先函数导数,再求导函数零点,列表分析导函数符号变化规律,进而确定单调区间和极值
(2)先函数导数,再求导函数零点,列表分析导函数符号变化规律,进而确定单调区间和极值
试题解析:(1)![]() ,切线为
,切线为![]() ,即斜率
,即斜率![]() ,纵坐标
,纵坐标![]()
即![]() ,
, ![]() ,解得
,解得![]() ,
, ![]()
解析式![]()
(2)![]()
![]()
![]() ,定义域为
,定义域为![]()
得到![]() 在
在![]() 单增,在
单增,在![]() 单减,在
单减,在![]() 单增
单增
极大值![]() ,极小值
,极小值![]() .
.
【题型】解答题
【结束】
20
【题目】如图:在四棱锥![]() 中,底面
中,底面![]() 为菱形,且
为菱形,且![]() ,
, ![]() 底面
底面![]() ,
,
![]() ,
, ![]() ,
, ![]() 是
是![]() 上点,且
上点,且![]() 平面
平面![]() .
.
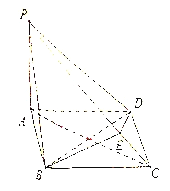
(1)求证: ![]() ;(2)求三棱锥
;(2)求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在框图中,设x=2,并在输入框中输入n=4;ai=i(i=0,1,2,3,4).则此程序执行后输出的S值为( ) 
A.26
B.49
C.52
D.98
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的两个焦点分别为
的两个焦点分别为![]() ,
, ![]() ,且点
,且点 在椭圆
在椭圆![]() 上.
上.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设椭圆![]() 的左顶点为
的左顶点为![]() ,过点
,过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于异于
相交于异于![]() 的不同两点
的不同两点![]() ,求
,求![]() 的面积
的面积![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知{an}为等差数列,前n项和为Sn(n∈N*),{bn}是首项为2的等比数列,且公比大于0,b2+b3=12,b3=a4-2a1,S11=11b4.
(Ⅰ)求{an}和{bn}的通项公式;
(Ⅱ)求数列{a2nbn}的前n项和(n∈N*).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com