
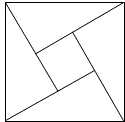
 2002年8月,在北京召开的国际数学家大会会标如图所示,它是由4个相同的直角三角形与中间的小正方形拼成的一个大正方形,若直角三角形中较小的锐角为θ,大正方形的面积是1,小正方形的面积是
2002年8月,在北京召开的国际数学家大会会标如图所示,它是由4个相同的直角三角形与中间的小正方形拼成的一个大正方形,若直角三角形中较小的锐角为θ,大正方形的面积是1,小正方形的面积是| 1 | 25 |
| 1 |
| 25 |
| 1 |
| 25 |
| 1 |
| 5 |
| 1 |
| 25 |
| 24 |
| 25 |
| 49 |
| 25 |
| 49 |
| 25 |
| 7 |
| 5 |
| 7 |
| 25 |
| 7 |
| 25 |


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案科目:高中数学 来源: 题型:
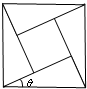 2002年8月,在北京召开国际数学家大会,大会会标如图所示,它是由四个相同的直角三角形、与中间的小正方形拼成的大正方形.若直角三角形中较小的锐角为θ,大正方形的面积为1,小正方形的面积为
2002年8月,在北京召开国际数学家大会,大会会标如图所示,它是由四个相同的直角三角形、与中间的小正方形拼成的大正方形.若直角三角形中较小的锐角为θ,大正方形的面积为1,小正方形的面积为| 1 |
| 25 |
| 7 |
| 5 |
| 7 |
| 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 2002年8月,在北京召开的国际数学家大会会标如图所示,它是由4个相同的直角三角形与中间的小
2002年8月,在北京召开的国际数学家大会会标如图所示,它是由4个相同的直角三角形与中间的小| 1 | 25 |
查看答案和解析>>
科目:高中数学 来源: 题型:
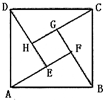 2002年8月,在北京召开的国际数学家大会会标如图所示,它是由4个相同的直角三角形与中间的小正方形拼成的一大正方形,若直角三角形中较大的锐角为θ,大正方形的面积是1,小正方形的面积是
2002年8月,在北京召开的国际数学家大会会标如图所示,它是由4个相同的直角三角形与中间的小正方形拼成的一大正方形,若直角三角形中较大的锐角为θ,大正方形的面积是1,小正方形的面积是| 1 | 25 |
查看答案和解析>>
科目:高中数学 来源:2010-2011年陕西省西安市高一下学期第二次月考数学 题型:选择题
2002年8月,在北京召开的国际数学家大会会标如图所示,它是由4个相同的直角三角形与中间的小正方形拼成的一大正方形,若直角三角形中较小的锐角为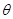 ,大正方形的面积是1,小正方形的面积是
,大正方形的面积是1,小正方形的面积是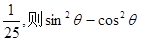 的值等于( )
的值等于( )
A.1 B.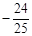 C.
C.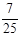 D.
D.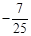
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com