
(1)求实数b的取值范围;
(2)若函数F(x)=logbf(x)在区间(-1-c,1-c)上具有单调性,求实数c的取值范围.
(文)已知二次函数f(x)=x2+2bx+c(b、c∈R).
(1)若f(x)≤0的解集为{x|-1≤x≤1},求实数b、c的值;
(2)若f(x)满足f(1)=0,且关于x的方程f(x)+x+b=0的两个实数根分别在区间(-3,-2)、(0,1)内,求实数b的取值范围.
答案:(理)解:(1)由题,知f(1)=1+2b+c=0,∴c=-1-2b.
记g(x)=f(x)+x+b=x2+(2b+1)x+b+c=x2+(2b+1)x-b-1,
则 即b∈(
即b∈(![]() ).
).
(2)令u=f(x).∵0<![]() <b<
<b<![]() <1,∴logbu在(0,+∞)上是减函数.而-1-c=2b>-b,函数f(x)=x2+2bx+c的对称轴为x=-b,∴f(x)在区间(-1-c,1-c)上单调递增.从而函数F(x)=logbf(x)在(-1-c,1-c)上为减函数.
<1,∴logbu在(0,+∞)上是减函数.而-1-c=2b>-b,函数f(x)=x2+2bx+c的对称轴为x=-b,∴f(x)在区间(-1-c,1-c)上单调递增.从而函数F(x)=logbf(x)在(-1-c,1-c)上为减函数.
且f(x)在区间(-1-c,1-c)上恒有f(x)>0,只需要f(-1-c)≥0,
∴ .
.
(文)解:(1)由题,知x1=-1,x2=1是方程x2+2bx+c=0的两个根.
由韦达定理,得
即![]() ∴b=0,c=-1.
∴b=0,c=-1.
(2)由题,知f(1)=1+2b+c=0,∴c=-1-2b.2分记g(x)=f(x)+x+b=x2+(2b+1)x+b+c=x2+(2b+1)x-b-1,则
 即b∈(
即b∈(![]() ,
,![]() ).
).


 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:高中数学 来源: 题型:
| 1 |
| 8 |
| 1 |
| 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
(09年宜昌一中12月月考理)(14分)
已知二次函数![]() 。
。
(1)若对任意x1,x2∈R,且![]() ,都有
,都有![]() ,求证:关于x的方程
,求证:关于x的方程![]() 有两个不相等的实数根且必有一个根属于(
有两个不相等的实数根且必有一个根属于(![]() );
);
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
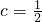 时,求出不等式f(x)<0的解;
时,求出不等式f(x)<0的解;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com