练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知函数，其中，，则下列选项中的条件使得仅有一个零点的有（ ）

    A.为奇函数B.

    C.，D.，

    【答案】BD

    【解析】

    利用导数得出函数的极值点结合奇函数的性质，即可得出有三个零点，错误；

    由，得出，从而得出函数单调递增，则B正确；

    取，利用导数得出的极大值为，极小值为，从而得出有两个零点，错误；

    得出函数的极大值和极小值，并判断其正负，即可得出仅有一个零点，正确.

    由题知.

    对于，由是奇函数，知，因为，所以存在两个极值点，由知，有三个零点，错误；

    对于，因为，所以，，所以单调递增，则仅有一个零点，正确；

    对于，若取，，则的极大值为，极小值为，此时有两个零点，错误；

    对于，，

    易得的极大值为，极小值为.

    可知仅有一个零点，正确.

    故选：BD

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】[选修4-4：坐标系与参数方程]

    在直角坐标系中，曲线:（，为参数）.在以坐标原点为极点，轴的正半轴为极轴的极坐标系中，曲线：.

    （1）说明是哪一种曲线，并将的方程化为极坐标方程；

    （2）若直线的方程为，设与的交点为，，与的交点为，，若的面积为，求的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】“搜索指数”是网民通过搜索引擎，以每天搜索关键词的次数为基础所得到的统计指标.“搜索指数”越大，表示网民对该关键词的搜索次数越多，对该关键词相关的信息关注度也越高.下图是2017年9月到2018年2月这半年中，某个关键词的搜索指数变化的走势图.

    根据该走势图，下列结论正确的是（ ）

    A. 这半年中，网民对该关键词相关的信息关注度呈周期性变化

    B. 这半年中，网民对该关键词相关的信息关注度不断减弱

    C. 从网民对该关键词的搜索指数来看，去年10月份的方差小于11月份的方差

    D. 从网民对该关键词的搜索指数来看，去年12月份的平均值大于今年1月份的平均值

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示七面体中，，平面，平面平面，四边形是边长为2的菱形，，，M，N分别为，的中点.

    （1）求证：平面；

    （2）求三棱锥的体积.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示，在平行四边形ABCD中，，，，点E是CD边的中点，将沿AE折起，使点D到达点P的位置，且.

    （1）求证；平面平面ABCE；

    （2）求点E到平面PAB的距离.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知、分别是离心率的椭圆的左右项点，P是椭圆E的上顶点，且.

    （1）求椭圆E的方程；

    （2）若动直线过点，且与椭圆E交于A、B两点，点M与点B关于y轴对称，求证：直线恒过定点.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图：已知四棱锥P—ABCD的底面ABCD是平行四边形，PA⊥面ABCD，M是AD的中点，N是PC的中点.

    （1）求证：MN∥面PAB；

    （2）若平面PMC⊥面PAD，求证：CM⊥AD.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，．

    （1）若函数与的图象上存在关于原点对称的点，求实数的取值范围；

    （2）设，已知在上存在两个极值点，，且，求证：（其中为自然对数的底数）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

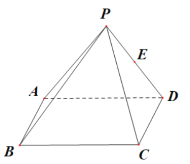
    【题目】如图，在四棱锥中，底面为矩形，，侧面为等边三角形且垂直于底面，是的中点.

    （1）在棱上取一点使直线∥平面并证明；

    （2）在（1）的条件下，当棱上存在一点，使得直线与底面所成角为时，求二面角的余弦值.

    查看答案和解析>>

    同步练习册答案