【题目】设锐角△ABC的三个内角为A，B，C，其中角B的大小为 
，则cosA+sinC的取值范围为 ．
【答案】
【解析】解：设锐角三角形ABC的三个内角分别为A，B，C， 则A+B+C=π，0＜A＜ 
，0＜B＜ ，0＜C＜ ，
∵B= 
，∴A+C= 
，
∴ 
＜A＜ ， ＜C＜ ，
∴cosA+sinC=cos（ ﹣C）+sinC=﹣ 
cosC+ 
sinC+sinC=﹣ cosC+ 
sinC，
∵﹣ cosC+ sinC= 
（sinCcos ﹣cosCsin ）= sin（C﹣ ），
又 ＜C＜ ，
∴ =sin ＜sin（C﹣ ）＜sin = ，
∴ ＜cosA+sinC＜ ，
cosA+sinC的取值范围是 ．
所以答案是： ．
【考点精析】认真审题，首先需要了解两角和与差的余弦公式(两角和与差的余弦公式：
)，还要掌握余弦定理的定义(余弦定理:
;;
)的相关知识才是答题的关键．
暑假作业暑假快乐练西安出版社系列答案科目：高中数学 来源： 题型：
【题目】已知函数f（x）=2x3+bx2+cx，其导函数y=f′（x）的图象（如图所示）经过点（1，0），（2，0）． （Ⅰ）求f（x）的解析式；
（Ⅱ）若方程f（x）﹣m=0恰有2个根，求m的值．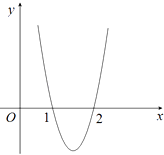
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】若将函数y=cos 2x的图象向左平移 
个单位长度，则平移后图象的对称轴为（ ）
A.x= 
﹣ 
（k∈Z）
B.x= + （k∈Z）
C.x= ﹣ （k∈Z）
D.x= + （k∈Z）
查看答案和解析>>
科目：高中数学 来源： 题型：
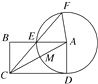
【题目】如图，在矩形ABCD中，以A为圆心，AD为半径的圆交AC，AB于M，E.CE的延长线交⊙A于F，CM＝2，AB＝4.
(1)求⊙A的半径；
(2)求CE的长和△AFC的面积
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）=x﹣alnx（a∈R）
（1）当a=2时，求曲线y=f（x）在点A（1，f（1））处的切线方程；
（2）求函数f（x）的极值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】若存在实常数
和
，使得函数
和
对其定义域上的任意实数
分别满足： 
和
，则称直线
为
和
的“隔离直线”．已知
， 
为自然对数的底数)．
（1）求
的极值；
（2）函数
和
是否存在隔离直线？若存在，求出此隔离直线方程；若不存在，请说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某同学用“五点法”画函数f（x）=Asin（ωx+φ）（ω＞0，|φ|＜ 
）在某一个周期内的图象时，列表并填入了部分数据，如表：
ωx+φ | 0 |
| π |
| 2π |
x |
|
| |||
Asin（ωx+φ） | 0 | 5 | ﹣5 | 0 |
（1）请将上表数据补充完整，填写在相应位置，并直接写出函数f（x）的解析式；
（2）将y=f（x）图象上所有点向左平行移动θ（θ＞0）个单位长度，得到y=g（x）的图象．若y=g（x）图象的一个对称中心为（ 
，0），求θ的最小值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
