
【题目】△ABC的内角A,B,C所对应的边分别为a,b,c.
(Ⅰ)若a,b,c成等差数列,证明:sinA+sinC=2sin(A+C);
(Ⅱ)若a,b,c成等比数列,求cosB的最小值.
【答案】(Ⅰ)详见解析(Ⅱ)![]()
【解析】
试题分析:(Ⅰ)由a,b,c成等差数列,利用等差数列的性质列出关系式,利用正弦定理化简,再利用诱导公式变形即可得证;(Ⅱ)由a,bc成等比数列,利用等比数列的性质列出关系式,再利用余弦定理表示出cosB,将得出的关系式代入,并利用基本不等式变形即可确定出cosB的最小值
试题解析:
(Ⅰ)∵a,b,c成等差数列,
∴2b=a+c,
利用正弦定理化简得:2sinB=sinA+sinC,
∵sinB=sin[π﹣(A+C)]=sin(A+C),
∴sinA+sinC=2sinB=2sin(A+C);
(Ⅱ)∵a,b,c成等比数列,
∴b2=ac,
∴cosB=![]() =
=![]() ≥
≥![]() =
=![]() ,
,
当且仅当a=c时等号成立,
∴cosB的最小值为![]() .
.


科目:高中数学 来源: 题型:
【题目】若有一个企业,70%的员工年收入1万元,25%的员工年收入3万元,5%的员工年收入11万元,则该企业员工的年收入的平均数是________万元,中位数是________万元,众数是________万元.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】类比平面几何中的命题:“垂直于同一直线的两条直线平行”,在立体几何中,可以得到命题“__________”,这个类比命题的真假性是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,
,![]() .
.
(1)求![]() 的极值;
的极值;
(2)设![]() ≤
≤![]() ,记
,记![]() 在
在![]() 上的最大值为
上的最大值为![]() ,求函数
,求函数![]() 的最小值;
的最小值;
(3)设函数![]() (
(![]() 为常数),若使
为常数),若使![]() ≤
≤![]() ≤
≤![]() 在
在![]() 上恒成立的实数
上恒成立的实数![]() 有且只有一个,求实数
有且只有一个,求实数![]() 和
和![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国乒乓球队备战里约奥运会热身赛暨选拔赛于2016年7月14日在山东威海开赛.种子选手![]() 与
与![]() ,
,![]() ,
,![]() 三位非种子选手分别进行一场对抗赛,按以往多次比赛的统计,
三位非种子选手分别进行一场对抗赛,按以往多次比赛的统计,![]() 获胜的概率分别为
获胜的概率分别为![]() ,
,![]() ,
,![]() ,且各场比赛互不影响.
,且各场比赛互不影响.
(1)若![]() 至少获胜两场的概率大于
至少获胜两场的概率大于![]() ,则
,则![]() 入选征战里约奥运会的最终大名单,否则不予入选,问
入选征战里约奥运会的最终大名单,否则不予入选,问![]() 是否会入选最终的大名单?
是否会入选最终的大名单?
(2)求![]() 获胜场数
获胜场数![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】 用反证法证明命题:“三角形三个内角至少有一个不大于60°”时,应假设( )
A.三个内角都不大于60° B.三个内角都大于60°
C.三个内角至多有一个大于60° D.三个内角至多有两个大于60°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,当点
,当点![]() 在
在![]() 的图象上运动时,点
的图象上运动时,点![]() 在函数
在函数![]() 的图象上运动(
的图象上运动(![]() ).
).
(Ⅰ)求![]() 和
和![]() 的表达式;
的表达式;
(Ⅱ)已知关于![]() 的方程
的方程![]() 有实根,求实数
有实根,求实数![]() 的取值范围;
的取值范围;
(Ⅲ)设![]() ,函数
,函数![]() 的值域为
的值域为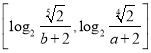 ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com