
【题目】已知函数f(x)=cosωx(sinωx+ ![]() cosωx)(ω>0),如果存在实数x0 , 使得对任意的实数x,都有f(x0)≤f(x)≤f(x0+2016π)成立,则ω的最小值为( )
cosωx)(ω>0),如果存在实数x0 , 使得对任意的实数x,都有f(x0)≤f(x)≤f(x0+2016π)成立,则ω的最小值为( )
A.![]()
B.![]()
C.![]()
D.![]()
 黄冈创优卷系列答案
黄冈创优卷系列答案科目:高中数学 来源: 题型:
【题目】先把正弦函数y=sinx图象上所有的点向左平移 ![]() 个长度单位,再把所得函数图象上所有的点的纵坐标缩短到原来的
个长度单位,再把所得函数图象上所有的点的纵坐标缩短到原来的 ![]() 倍(横坐标不变),再将所得函数图象上所有的点的横坐标缩短到原来的
倍(横坐标不变),再将所得函数图象上所有的点的横坐标缩短到原来的 ![]() 倍(纵坐标不变),则所得函数图象的解析式是( )
倍(纵坐标不变),则所得函数图象的解析式是( )
A.y=2sin( ![]() x+
x+ ![]() )
)
B.y= ![]() sin(2x﹣
sin(2x﹣ ![]() )
)
C.y=2sin( ![]() x﹣
x﹣ ![]() )
)
D.y= ![]() sin(2x+
sin(2x+ ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是边长为2的正方形,侧面PAD⊥底面ABCD,且PA=PD= ![]() AD.
AD. 
(1)求证:平面PAB⊥平面PDC
(2)在线段AB上是否存在一点G,使得二面角C﹣PD﹣G的余弦值为 ![]() .若存在,求
.若存在,求 ![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=Asin(ωx+φ)(A>0,ω>0)的图象如图所示,则以下步骤可以得到函数f(x)的图象的是( ) 
A.将y=sinx的图象上的点纵坐标不变,横坐标变成原来的2倍,然后再向左平移 ![]() 个单位
个单位
B.将y=sinx的图象上的点纵坐标不变,横坐标变成原来的2倍,然后再向右平移 ![]() 个单位
个单位
C.将y=sinx的图象上的点纵坐标不变,横坐标变成原来的 ![]() ,然后再向右平移
,然后再向右平移 ![]() 个单位
个单位
D.将y=sinx的图象上的点纵坐标不变,横坐标变成原来的 ![]() ,然后再向左平移
,然后再向左平移 ![]() 个单位
个单位
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对某个品牌的U盘进行寿命追踪调查,所得情况如下面频率分布直方图所示. 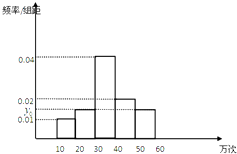
(1)图中纵坐标y0处刻度不清,根据图表所提供的数据还原y0;
(2)根据图表的数据按分层抽样,抽取20个U盘,寿命为1030万次之间的应抽取几个;
(3)从(2)中抽出的寿命落在1030万次之间的元件中任取2个元件,求事件“恰好有一个寿命为1020万次,一个寿命为2030万次”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某小区抽取100户居民进行月用电量调查,发现其用电量都在50至350度之间,频率分布直方图如图所示,在这些用户中,用电量落在区间[150,250)内的户数为 . 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)在R上存在导数f′(x),x∈R,有f(﹣x)+f(x)=x2 , 在(0,+∞)上f′(x)<x,若f(4﹣m)﹣f(m)≥8﹣4m.则实数m的取值范围为( )
A.[﹣2,2]
B.[2,+∞)
C.[0,+∞)
D.(﹣∞,﹣2]∪[2,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() .(x>0)
.(x>0)
(1)函数f(x)在区间(0,+∞)上是增函数还是减函数?证明你的结论;
(2)若当x>0时,f(x)> ![]() 恒成立,求正整数k的最大值.
恒成立,求正整数k的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合M是R的子集,如果点x0∈R满足:a>0,x∈M,0<|x﹣x0|<a,称x0为集合M的聚点.则下列集合中以1为聚点的有( ) ① ![]() ;
;
② ![]() ;
;
③Z;
④{y|y=2x}.
A.①④
B.②③
C.①②
D.①②④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com