
分析 因为正三角形ABC的外径r=2,故可以得到高,D是BC的中点.在△OBC中,又可以得到角以及边与R的关系,在Rt△ABD中,再利用直角三角形的勾股定理,即可解出R.
解答 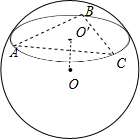 解:因为正三角形ABC的外径r=2,故高AD=$\frac{3}{2}$r=3,D是BC的中点.
解:因为正三角形ABC的外径r=2,故高AD=$\frac{3}{2}$r=3,D是BC的中点.
在△OBC中,BO=CO=R,∠BOC=$\frac{π}{3}$,所以BC=BO=R,BD=$\frac{1}{2}$BC=$\frac{1}{2}$R.
在Rt△ABD中,AB=BC=R,所以由AB2=BD2+AD2,得R2=$\frac{1}{4}$R2+9,所
以R=2$\sqrt{3}$.
点评 本题考查学生的空间想象能力,以及对球的性质认识及利用,是基础题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若a+b≠1,则a2+b2<$\frac{1}{2}$ | B. | 若a+b=1,则a2+b2<$\frac{1}{2}$ | ||
| C. | 若a2+b2<$\frac{1}{2}$,则a+b≠1 | D. | 若a2+b2≥$\frac{1}{2}$,则a+b=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-6]∪[2,+∞) | B. | (-∞,-4)∪(4,+∞) | C. | [2,+∞) | D. | [-6,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
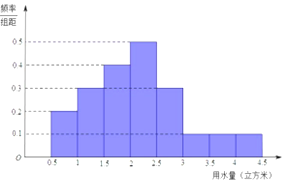 某市为鼓励居民节约用水,拟实行阶梯水价,每人用水量中不超过w 立方米按2 元/立方米收费,超出w 立方米但不高于w+2 的部分按4 元/立方米收费,超出w+2 的部分按8 元/立方米收费,从该市随机调查了10000 位居民,获得了他们某月的用水量数据,整理得到如图所示频率分布直方图:
某市为鼓励居民节约用水,拟实行阶梯水价,每人用水量中不超过w 立方米按2 元/立方米收费,超出w 立方米但不高于w+2 的部分按4 元/立方米收费,超出w+2 的部分按8 元/立方米收费,从该市随机调查了10000 位居民,获得了他们某月的用水量数据,整理得到如图所示频率分布直方图:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com