
【题目】将圆x2+y2=1上每一点的横坐标保持不变,纵坐标变为原来的2倍,得曲线C.
(1)写出C的参数方程;
(2)设直线l:2x+y﹣2=0与C的交点为P1 , P2 , 以坐标原点为极点,x轴正半轴为极轴建立极坐标系,求过线段P1P2的中点且与l垂直的直线的极坐标方程.
【答案】
(1)解:在曲线C上任意取一点(x,y),由题意可得点(x, ![]() )在圆x2+y2=1上,
)在圆x2+y2=1上,
∴x2+ ![]() =1,即曲线C的方程为 x2+
=1,即曲线C的方程为 x2+ ![]() =1,化为参数方程为
=1,化为参数方程为 ![]() (0≤θ<2π,θ为参数).
(0≤θ<2π,θ为参数).
(2)解:由 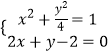 ,可得
,可得 ![]() ,
, ![]() ,不妨设P1(1,0)、P2(0,2),
,不妨设P1(1,0)、P2(0,2),
则线段P1P2的中点坐标为( ![]() ,1),
,1),
再根据与l垂直的直线的斜率为 ![]() ,故所求的直线的方程为y﹣1=
,故所求的直线的方程为y﹣1= ![]() (x﹣
(x﹣ ![]() ),即x﹣2y+
),即x﹣2y+ ![]() =0.
=0.
再根据x=ρcosα、y=ρsinα 可得所求的直线的极坐标方程为ρcosα﹣2ρsinα+ ![]() =0,
=0,
即 ρ= ![]()
【解析】(1)在曲线C上任意取一点(x,y),再根据点(x, ![]() )在圆x2+y2=1上,求出C的方程,化为参数方程.(2)解方程组求得P1、P2的坐标,可得线段P1P2的中点坐标.再根据与l垂直的直线的斜率为
)在圆x2+y2=1上,求出C的方程,化为参数方程.(2)解方程组求得P1、P2的坐标,可得线段P1P2的中点坐标.再根据与l垂直的直线的斜率为 ![]() ,用点斜式求得所求的直线的方程,再根据x=ρcosα、y=ρsinα 可得所求的直线的极坐标方程.
,用点斜式求得所求的直线的方程,再根据x=ρcosα、y=ρsinα 可得所求的直线的极坐标方程.


科目:高中数学 来源: 题型:
【题目】已知抛物线C:y2=2px(p>0)的焦点为F,A为C上异于原点的任意一点,过点A的直线l交C于另一点B,交x轴的正半轴于点D,且有丨FA丨=丨FD丨.当点A的横坐标为3时,△ADF为正三角形.
(1)求C的方程;
(2)若直线l1∥l,且l1和C有且只有一个公共点E,
(ⅰ)证明直线AE过定点,并求出定点坐标;
(ⅱ)△ABE的面积是否存在最小值?若存在,请求出最小值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是某单位职工的月收入情况画出的样本频率分布直方图,已知图中第一组的频数为4 000,请根据该图提供的信息,解答下列问题.
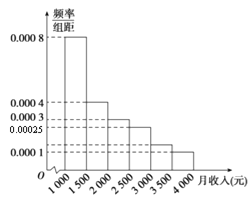
(1)为了分析职工的收入与年龄、学历等方面的关系,必须从样本中按月收入用分层抽样方法抽出100人作进一步分析,则月收入在[1 500,2 000)的这组中应抽取多少人?
(2)试估计样本数据的中位数与平均数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为庆祝成立二十周年,特举办《快乐大闯关》竞技类有奖活动,该活动共有四关,由两名男职员与两名女职员组成四人小组,设男职员闯过一至四关概率依次是![]() ,女职员闯过一至四关的概率依次是
,女职员闯过一至四关的概率依次是![]()
(1)求女职员闯过四关的概率;
(2)设![]() 表示四人小组闯过四关的人数,求随机变量
表示四人小组闯过四关的人数,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,
,![]() 是函数
是函数![]() (
(![]() ,
,![]() )图象上的任意两点,且角
)图象上的任意两点,且角![]() 的终边经过点
的终边经过点![]() ,若
,若![]() 时,
时,![]() 的最小值为
的最小值为![]() .
.
(1)求函数![]() 的解析式;
的解析式;
(2)当![]() 时,不等式
时,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是一个半圆形湖面景点的平面示意图.已知![]() 为直径,且
为直径,且![]() km,
km,![]() 为圆心,
为圆心,![]() 为圆周上靠近
为圆周上靠近![]() 的一点,
的一点,![]() 为圆周上靠近
为圆周上靠近![]() 的一点,且
的一点,且![]() ∥
∥![]() .现在准备从
.现在准备从![]() 经过
经过![]() 到
到![]() 建造一条观光路线,其中
建造一条观光路线,其中![]() 到
到![]() 是圆弧
是圆弧![]() ,
,![]() 到
到![]() 是线段
是线段![]() .设
.设![]() ,观光路线总长为
,观光路线总长为![]() .
.

(1)求![]() 关于
关于![]() 的函数解析式,并指出该函数的定义域;
的函数解析式,并指出该函数的定义域;
(2)求观光路线总长的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com