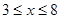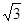试题分析:解:将直线2ρcosθ=1化为普通方程为:2x=1.∵ρ=2cosθ,∴ρ
2=2ρcosθ,化为普通方程为:x
2+y
2=2x,即(x-1)
2+y
2=1.∴直线与圆相交的弦长=
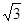
解:∵函数f(x)=|x-4|+|x-a|≥|x-4+a-x|=|a-4|,∵f(x)的最小值为3,∴|a-4|=3,∴a=1或7,∵a>1,∴a=7,∴f(x)=|x-4|+|x-7|≤5,①若x≤4,f(x)=4-x+7-x=11-2x≤5,解得x≥3,故3≤x≤4;②若4<x<7,f(x)=x-4+7-x=3,恒成立,故4<x<7;③若x≥7,f(x)=x-4+x-7=2x-11≤5,解得x≤8,故7≤x≤8;
综上3≤x≤8,故答案为:3≤x≤8.
点评:主要是考查了不等式选讲以及坐标系与参数方程的运用,属于基础题。

 与圆
与圆 相交的弦长为 .
相交的弦长为 .
 >1),且
>1),且 的最小值为
的最小值为 ,若
,若 ,则
,则 的取值范围
的取值范围 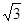 (Ⅱ)
(Ⅱ)