
【题目】设函数f(x)= ![]() ﹣k(
﹣k( ![]() +lnx)(k为常数,e=2.71828…是自然对数的底数). (Ⅰ)当k≤0时,求函数f(x)的单调区间;
+lnx)(k为常数,e=2.71828…是自然对数的底数). (Ⅰ)当k≤0时,求函数f(x)的单调区间;
(Ⅱ)若函数f(x)在(0,2)内存在两个极值点,求k的取值范围.
【答案】解:(Ⅰ)f(x)的定义域为(0,+∞), ∴f′(x)= ![]() ﹣k(
﹣k( ![]() ﹣
﹣ ![]() )
)
= ![]() (x>0),
(x>0),
当k≤0时,kx≤0,
∴ex﹣kx>0,
令f′(x)=0,则x=2,
∴当0<x<2时,f′(x)<0,f(x)单调递减;
当x>2时,f′(x)>0,f(x)单调递增,
∴f(x)的单调递减区间为(0,2),单调递增区间为(2,+∞).
(Ⅱ)由(Ⅰ)知,k≤0时,函数f(x)在(0,2)内单调递减,
故f(x)在(0,2)内不存在极值点;
当k>0时,设函数g(x)=ex﹣kx,x∈(0,+∞).
∵g′(x)=ex﹣k=ex﹣elnk ,
当0<k≤1时,
当x∈(0,2)时,g′(x)=ex﹣k>0,y=g(x)单调递增,
故f(x)在(0,2)内不存在两个极值点;
当k>1时,
得x∈(0,lnk)时,g′(x)<0,函数y=g(x)单调递减,
x∈(lnk,+∞)时,g′(x)>0,函数y=g(x)单调递增,
∴函数y=g(x)的最小值为g(lnk)=k(1﹣lnk)
函数f(x)在(0,2)内存在两个极值点
当且仅当 
解得:e ![]()
综上所述,
函数f(x)在(0,2)内存在两个极值点时,k的取值范围为(e, ![]() )
)
【解析】(Ⅰ)求出导函数,根据导函数的正负性,求出函数的单调区间;(Ⅱ)函数f(x)在(0,2)内存在两个极值点,等价于它的导函数f′(x)在(0,2)内有两个不同的零点.
【考点精析】通过灵活运用利用导数研究函数的单调性和函数的极值,掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;极值反映的是函数在某一点附近的大小情况即可以解答此题.
在这个区间单调递减;极值反映的是函数在某一点附近的大小情况即可以解答此题.


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:高中数学 来源: 题型:
【题目】某单位安排![]() 位员工在春节期间大年初一到初七值班,每人值班
位员工在春节期间大年初一到初七值班,每人值班![]() 天,若
天,若![]() 位员工中的甲、乙排在相邻的两天,丙不排在初一,丁不排在初七,则不同的安排方案共有_______
位员工中的甲、乙排在相邻的两天,丙不排在初一,丁不排在初七,则不同的安排方案共有_______
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分) 某中学的环保社团参照国家环境标准制定了该校所在区域空气质量指数与空气质量等级对应关系如下表(假设该区域空气质量指数不会超过![]() ):
):
空气质量指数 |
|
|
|
|
|
|
空气质量等级 |
|
|
|
|
|
|
该社团将该校区在![]() 年
年![]() 天的空气质量指数监测数据作为样本,绘制的频率分布直方图如下图,把该直方图所得频率估计为概率.
天的空气质量指数监测数据作为样本,绘制的频率分布直方图如下图,把该直方图所得频率估计为概率.
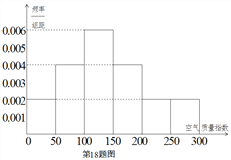
(Ⅰ)请估算![]() 年(以
年(以![]() 天计算)全年空气质量优良的天数(未满一天按一天计算);
天计算)全年空气质量优良的天数(未满一天按一天计算);
(Ⅱ)该校![]() 年
年![]() 月
月![]() 、
、![]() 日将作为高考考场,若这两天中某天出现
日将作为高考考场,若这两天中某天出现![]() 级重度污染,需要净化空气费用
级重度污染,需要净化空气费用![]() 元,出现
元,出现![]() 级严重污染,需要净化空气费用
级严重污染,需要净化空气费用![]() 元,记这两天净化空气总费用为
元,记这两天净化空气总费用为![]() 元,求
元,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x),g(x)的定义域都是D,直线x=x0(x0∈D),与y=f(x),y=g(x)的图象分别交于A,B两点,若|AB|的值是不等于0的常数,则称曲线 y=f(x),y=g(x)为“平行曲线”,设f(x)=ex﹣alnx+c(a>0,c≠0),且y=f(x),y=g(x)为区间(0,+∞)的“平行曲线”,g(1)=e,g(x)在区间(2,3)上的零点唯一,则a的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() ,在
,在![]() 处的切线方程为
处的切线方程为![]() .
.
(1)求![]() ,
, ![]() ;
;
(2)若![]() ,证明:
,证明: ![]() .
.
【答案】(1)![]() ,
, ![]() ;(2)见解析
;(2)见解析
【解析】试题分析:(1)求出函数的导数,得到关于![]() 的方程组,解出即可;
的方程组,解出即可;
(2)由(1)可知![]() ,
, ![]() ,
,
由![]() ,可得
,可得![]() ,令
,令![]() , 利用导数研究其单调性可得
, 利用导数研究其单调性可得
![]() ,
,
从而证明![]() .
.
试题解析:((1)由题意![]() ,所以
,所以![]() ,
,
又![]() ,所以
,所以![]() ,
,
若![]() ,则
,则![]() ,与
,与![]() 矛盾,故
矛盾,故![]() ,
, ![]() .
.
(2)由(1)可知![]() ,
, ![]() ,
,
由![]() ,可得
,可得![]() ,
,
令![]() ,
,
![]() ,
,
令![]()
当![]() 时,
时, ![]() ,
, ![]() 单调递减,且
单调递减,且![]() ;
;
当![]() 时,
时, ![]() ,
, ![]() 单调递增;且
单调递增;且![]() ,
,
所以![]() 在
在![]() 上当单调递减,在
上当单调递减,在![]() 上单调递增,且
上单调递增,且![]() ,
,
故![]() ,
,
故![]() .
.
【点睛】本题考查利用函数的切线求参数的方法,以及利用导数证明不等式的方法,解题时要认真审题,注意导数性质的合理运用.
【题型】解答题
【结束】
22
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为 (
(![]() ,
, ![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点, ![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() ,若直线
,若直线![]() 与曲线
与曲线![]() 相切;
相切;
(1)求曲线![]() 的极坐标方程;
的极坐标方程;
(2)在曲线![]() 上取两点
上取两点![]() ,
, ![]() 与原点
与原点![]() 构成
构成![]() ,且满足
,且满足![]() ,求面积
,求面积![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() :
:![]() (
(![]() 为参数),曲线
为参数),曲线![]() :
:![]() (
(![]() 为参数).
为参数).
(1)设![]() 与
与![]() 相交于
相交于![]() ,
,![]() 两点,求
两点,求![]() 的值;
的值;
(2)若把曲线![]() 上各点的横坐标压缩为原来的
上各点的横坐标压缩为原来的![]() ,纵坐标压缩为原来的
,纵坐标压缩为原来的![]() ,得到曲线
,得到曲线![]() ,设点
,设点![]() 是曲线
是曲线![]() 上的一个动点,求它到直线
上的一个动点,求它到直线![]() 的距离的最小值.
的距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于圆周率π,数学发展史上出现过许多很有创意的求法,如著名的蒲丰实验和查理斯实验.受其启发,我们也可以通过设计下面的实验来估计π的值:先请200名同学,每人随机写下一个都小于1 的正实数对(x,y);再统计两数能与1构成钝角三角形三边的数对(x,y)的个数m;最后再根据统计数m来估计π的值.假如统计结果是m=56,那么可以估计π≈ . (用分数表示)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x+1|﹣|x﹣2|.
(Ⅰ)求不等式f(x)≥1的解集;
(Ⅱ)若不等式f(x)≥x2﹣x+m的解集非空,求m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com