
【题目】已知函数![]() 为奇函数.
为奇函数.
(1)求实数![]() 的值;
的值;
(2)用定义法讨论并证明函数![]() 的单调性.
的单调性.
【答案】(1)![]() (2)
(2)![]() 在定义域
在定义域![]() 上为减函数,证明见解析
上为减函数,证明见解析
【解析】
(1)根据奇函数的定义![]() ,得出
,得出![]() ,化简得到
,化简得到![]() ,从而得到
,从而得到![]() 或1,再判断函数定义域是否关于原点对称,即可确定实数
或1,再判断函数定义域是否关于原点对称,即可确定实数![]() 的值;
的值;
(2) 令![]() ,利用作差法比较
,利用作差法比较![]() ,
,![]() 的大小,再根据对数函数的单调性得
的大小,再根据对数函数的单调性得![]() ,即
,即![]() ,结合函数单调性的定义,即可判断函数
,结合函数单调性的定义,即可判断函数![]() 的单调性.
的单调性.
解:(1)由![]() 及函数
及函数![]() 为奇函数可知
为奇函数可知![]() ,
,
有![]() ,得
,得![]()
有![]() ,得
,得![]() ,得
,得![]() ,故有
,故有![]() 或1,
或1,
①当![]() 时,
时,![]() ,此时函数定义域为
,此时函数定义域为![]() ,不关于原点对称,不可能是奇函数,
,不关于原点对称,不可能是奇函数,
②当![]() 时,
时,![]() ,令
,令![]() ,可得
,可得![]() ,故此时函数
,故此时函数![]() 的定义域为
的定义域为![]() 关于原点对称,函数
关于原点对称,函数![]() 为奇函数.
为奇函数.
由上知![]() .
.
(2)由(1)知![]() ,
,
令![]() ,有
,有![]()
![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ,可得
,可得![]() ,即
,即![]() ,
,
利用对数函数的单调性得![]() ,即
,即![]() ,
,
故函数![]() 在定义域
在定义域![]() 上为减函数.
上为减函数.


科目:高中数学 来源: 题型:
【题目】给定空间中十个点,其中任意四点不在一个平面上,将某些点之间用线段相连,若得到的图形中没有三角形也没有空间四边形,试确定所连线段数目的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在底面半径为6的圆柱内,有两个半径也为6的球面,两球的球心距为13,若作一个平面与两个球都相切,且与圆柱面相交成一椭圆,则椭圆的长轴长为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图为某大河的一段支流,岸线![]() 近似满足
近似满足![]() ∥
∥![]() 宽度为7
宽度为7![]() 圆
圆![]() 为河中的一个半径为2
为河中的一个半径为2![]() 的小岛,小镇
的小岛,小镇![]() 位于岸线
位于岸线![]() 上,且满足岸线
上,且满足岸线![]() 现计划建造一条自小镇
现计划建造一条自小镇![]() 经小岛
经小岛![]() 至对岸
至对岸![]() 的通道
的通道![]() (图中粗线部分折线段,
(图中粗线部分折线段,![]() 在
在![]() 右侧),为保护小岛,
右侧),为保护小岛,![]() 段设计成与圆
段设计成与圆![]() 相切,设
相切,设![]()
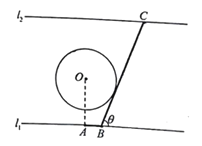
(1)试将通道![]() 的长
的长![]() 表示成
表示成![]() 的函数,并指出其定义域.
的函数,并指出其定义域.
(2)求通道![]() 的最短长.
的最短长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在抗击新型冠状病毒肺炎期间,为响应政府号召,郴州市某单位组织了志愿者30人,其中男志愿者18人,用分层抽样的方法从该单位志愿者中抽取5人去参加某社区的防疫帮扶活动.
(1)求从该单位男、女志愿者中各抽取的人数;
(2)从抽取的5名志愿者中任选2名谈此活动的感受,求选出的2名志愿者中恰有1名男志愿者的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】正四棱锥![]() 的底面正方形边长是3,
的底面正方形边长是3,![]() 是在底面上的射影,
是在底面上的射影,![]() ,
,![]() 是
是![]() 上的一点,过
上的一点,过![]() 且与
且与![]() 、
、![]() 都平行的截面为五边形
都平行的截面为五边形![]() .
.
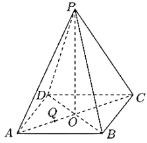
(1)在图中作出截面![]() ,并写出作图过程;
,并写出作图过程;
(2)求该截面面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知袋子中放有大小和形状相同的小球若干,其中标号为0的小球1个,标号为1的小球1个,标号为2的小球![]() 个.若从袋子中随机抽取1个小球,取到标号为2的小球的概率是
个.若从袋子中随机抽取1个小球,取到标号为2的小球的概率是![]() .
.
(1)求![]() 的值;
的值;
(2)从袋子中不放回地随机抽取2个小球,记第一次取出的小球标号为![]() ,第二次取出的小球标号为
,第二次取出的小球标号为![]() .
.
①记“![]() ”为事件
”为事件![]() ,求事件
,求事件![]() 的概率;
的概率;
②在区间![]() 内任取2个实数
内任取2个实数![]() ,
,![]() ,求事件“
,求事件“![]() 恒成立”的概率.
恒成立”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数y=2cos(2x+![]() )的图象向左平移
)的图象向左平移![]() 个单位长度,得到函数y=f(x)的图象.
个单位长度,得到函数y=f(x)的图象.
(1)求f(x)的单调递增区间;
(2)求f(x)在[0,![]() ]上的值域.
]上的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() x3-2x2+3x(x∈R)的图象为曲线C.
x3-2x2+3x(x∈R)的图象为曲线C.
(1)求过曲线C上任意一点切线斜率的取值范围;
(2)若在曲线C上存在两条相互垂直的切线,求其中一条切线与曲线C的切点的横坐标的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com