
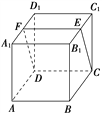
【题目】如图所示,在正方体ABCDA1B1C1D1中,E,F分别为B1C1,A1D1的中点.求证:平面ABB1A1与平面CDFE相交.
科目:高中数学 来源: 题型:
【题目】甲、乙、丙三人参加了一家公司的招聘面试,面试合格者可正式签约,甲表示只要面试合格就签约.乙、丙则约定:两人面试都合格就一同签约,否则两人都不签约.设甲、乙、丙面试合格的概率分别是![]() ,
, ![]() ,
, ![]() ,且面试是否合格互不影响.求:
,且面试是否合格互不影响.求:
(1)至少有1人面试合格的概率;
(2)签约人数![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中错误的是( )
A. 如果平面![]() 外的直线
外的直线![]() 不平行于平面
不平行于平面![]() ,则平面
,则平面![]() 内不存在与
内不存在与![]() 平行的直线
平行的直线
B. 如果平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
, ![]() ,那么直线
,那么直线![]() 平面
平面![]()
C. 如果平面![]() 平面
平面![]() ,那么平面
,那么平面![]() 内所有直线都垂直于平面
内所有直线都垂直于平面![]()
D. 一条直线与两个平行平面中的一个平面相交,则必与另一个平面相交
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋中有五张卡片,其中红色卡片三张,标号分别为1,2,3;蓝色卡片两张,标号分别为1,2.
(1)从以上五张卡片中任取两张,求这两张卡片颜色不同且标号之和小于4的概率;
(2)现袋中再放入一张标号为0的绿色卡片,从这六张卡片中任取两张,求这两张卡片颜色不同且标号之和小于4的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“菊花”型烟花是最壮观的烟花之一,制造时一般是期望在它达到最高点时爆裂.通过研究,发现该型烟花爆裂时距地面的高度![]() (单位:米)与时间
(单位:米)与时间![]() (单位:秒)存在函数关系,并得到相关数据如表:
(单位:秒)存在函数关系,并得到相关数据如表:
时间 | 1 |
|
|
高度 |
|
|
|
(1)根据表中数据,从下列函数中选取一个函数描述该型烟花爆裂时距地面的高度![]() 与时间
与时间![]() 的变化关系:
的变化关系: ![]() ,
, ![]() ,
, ![]() ,确定此函数解析式并简单说明理由;
,确定此函数解析式并简单说明理由;
(2)利用你选取的函数,判断烟花爆裂的最佳时刻,并求此时烟花距地面的高度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱锥A-BCD中,AB⊥平面BCD,CD⊥BD .

(1)求证:CD⊥平面ABD;
(2)若AB=BD=CD=1,M为AD中点,求三棱锥A-MBC的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两个篮球运动员互不影响地在同一位置投球,命中率分别为![]() 与
与![]() ,且乙投球3次均未命中的概率为
,且乙投球3次均未命中的概率为![]() ,甲投球未命中的概率恰是乙投球未命中的概率的2倍.
,甲投球未命中的概率恰是乙投球未命中的概率的2倍.
(Ⅰ)求乙投球的命中率![]() ;
;
(Ⅱ)若甲投球1次,乙投球2次,两人共命中的次数记为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com