
 .
.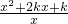 ,对?x1∈(0,+∞),?x2∈(-∞,0)使得f(x1)≤g(x2)成立,求正实数k的取值范围;
,对?x1∈(0,+∞),?x2∈(-∞,0)使得f(x1)≤g(x2)成立,求正实数k的取值范围; +
+ +…+
+…+ <
<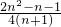 (n∈N*,n≥2)•
(n∈N*,n≥2)• -a,f′(2)=
-a,f′(2)= -a=-
-a=- ,解得a=1.
,解得a=1. -1=
-1=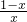 ,当x∈(0,1)时,f′(x)>0,f (x)为增函数,
,当x∈(0,1)时,f′(x)>0,f (x)为增函数,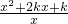 =x+
=x+ +2k=-(-x+
+2k=-(-x+ )+2k≤-2
)+2k≤-2 +2k,∴只须-2
+2k,∴只须-2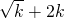 ≥0,解得k≥1.
≥0,解得k≥1. +
+ +…+
+…+ <
<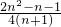 (n∈N*,n≥2)•
(n∈N*,n≥2)•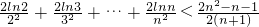 ,
,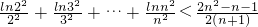 ,
,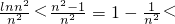 1-
1- =1-
=1-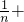
 ,
,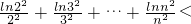 (1-
(1- +
+ )+(1-
)+(1- +
+ )+…+(1-
)+…+(1-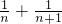 )
) +
+ =
=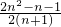 ,
, +
+ +…+
+…+ <
<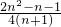 .
. 可求得a值,在定义域内解不等式f′(x)>0,f′(x)<0可求单调区间.
可求得a值,在定义域内解不等式f′(x)>0,f′(x)<0可求单调区间. +
+ +…+
+…+ <
<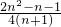 (n∈N*,n≥2),只须证
(n∈N*,n≥2),只须证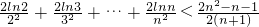 ,即证
,即证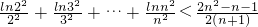 ,由f(x)的最大值得到一不等式,以此对该不等式左边各项进行放缩求和即可.
,由f(x)的最大值得到一不等式,以此对该不等式左边各项进行放缩求和即可.

 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2(x-1) |
| x+1 |
| x1+x2 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| f(n) |
查看答案和解析>>
科目:高中数学 来源: 题型:
| ||
| a |
| ||
| x |
| 6 |
| 6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com