
【题目】已知函数![]() ,
, ![]() .
.
(1)当![]() 时,求
时,求![]() 的单调递增区间;
的单调递增区间;
(2)设![]() ,且
,且![]() 有两个极值
有两个极值![]() ,其中
,其中![]() ,求
,求![]() 的最小值.
的最小值.
【答案】(1) ,当![]() 时F(x)的单增区间为(0,+
时F(x)的单增区间为(0,+![]() );当a
);当a![]() 1时,F(x)的单增区间为(0,
1时,F(x)的单增区间为(0, ![]() ),(
),(![]() );(2)
);(2) ![]() .
.
【解析】试题分析:
(1)求导得到![]() ,再设
,再设![]() 为目标函数进行分类讨论;(2)对
为目标函数进行分类讨论;(2)对![]() 求导得到
求导得到![]() 是
是![]() 的两根,所以根据韦达定理可以将双元问题转化为单元问题,从而设新函数求导即可解决问题。
的两根,所以根据韦达定理可以将双元问题转化为单元问题,从而设新函数求导即可解决问题。
试题解析:
(1)由题意得F(x)= x-![]() -2alnx. x
-2alnx. x![]() 0,
0, ![]() =
=![]() ,
,
令m(x)=x2-2ax+1, ![]()
①当![]() 时
时![]() F(x)在(0,+
F(x)在(0,+![]() 单调递增;
单调递增;
②当a![]() 1时,令
1时,令![]() ,得x1=
,得x1= ![]() , x2=
, x2= ![]()
x | (0, | ( | ( |
| + | - | + |
∴F(x)的单增区间为(0, ![]() ),(
),(![]() )
)
综上所述,当![]() 时F(x)的单增区间为(0,+
时F(x)的单增区间为(0,+![]() )
)
当a![]() 1时,F(x)的单增区间为(0,
1时,F(x)的单增区间为(0, ![]() ),(
),(![]() )
)
(2)h(x)= x-![]() 2alnx, h/(x)=
2alnx, h/(x)= ![]() ,(x>0),由题意知x1,x2是x2+2ax+1=0的两根,
,(x>0),由题意知x1,x2是x2+2ax+1=0的两根,
∴x1x2=1, x1+x2=-2a,x2=![]() ,2a=
,2a=![]() ,
,
![]() -
-![]() =
= ![]() -
-![]() =2(
=2(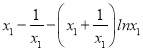 )
)
令H(x)=2(![]() ), H/(x)=2(
), H/(x)=2(![]() )lnx=
)lnx=![]()
当![]() 时,H/(x)<0, H(x)在
时,H/(x)<0, H(x)在![]() 上单调递减,H(x)的最小值为H(
上单调递减,H(x)的最小值为H(![]() )=
)=![]() ,
,
即![]() -
-![]() 的最小值为
的最小值为![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若![]() ,求曲线
,求曲线![]() 在点
在点![]() 处的切线;
处的切线;
(2)若函数![]() 在其定义域内为增函数,求正实数
在其定义域内为增函数,求正实数![]() 的取值范围;
的取值范围;
(3)设函数![]() ,若在
,若在![]() 上至少存在一点
上至少存在一点![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某人射击一次命中7~10环的概率如下表
命中环数 | 7 | 8 | 9 | 10 |
命中概率 | 0.16 | 0.19 | 0.28 | 0.24 |
计算这名射手在一次 射击中:
(1)射中10环或9环的概率;
(2)至少射中7环的概率;
(3)射中环数不足8环的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是椭圆
是椭圆![]() 的左右焦点,
的左右焦点,![]() 为原点,
为原点,![]()
![]() 在椭圆上,线段
在椭圆上,线段![]() 与
与![]() 轴的交点
轴的交点![]() 满足
满足![]() .
.
(1)求椭圆的标准方程;
(2)过椭圆右焦点![]() 作直线
作直线![]() 交椭圆于
交椭圆于![]() 两点,交
两点,交![]() 轴于
轴于![]() 点,若
点,若![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数y=f(x)的导数y′=f′(x)仍是x的函数,就把y′=f′(x)的导数y″=f″(x)叫做函数y=f(x)二阶导数,记做y(2)=f(2)(x).同样函数y=f(x)的n﹣1阶导数的导数叫做y=f(x)的n阶导数,表示y(n)=f(n)(x).在求y=ln(x+1)的n阶导数时,已求得 ![]() ,
, ![]() ,根据以上推理,函数y=ln(x+1)的第n阶导数为 .
,根据以上推理,函数y=ln(x+1)的第n阶导数为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂家举行大型的促销活动,经测算某产品当促销费用为![]() 万元时,销售量
万元时,销售量![]() 万件满足
万件满足![]() (其中
(其中![]() ,
, ![]() 为正常数),现假定生产量与销售量相等,已知生产该产品
为正常数),现假定生产量与销售量相等,已知生产该产品![]() 万件还需投入成本
万件还需投入成本![]() 万元(不含促销费用),产品的销售价格定为
万元(不含促销费用),产品的销售价格定为![]() 万元/万件.
万元/万件.
(1)将该产品的利润![]() 万元表示为促销费用
万元表示为促销费用![]() 万元的函数;
万元的函数;
(2)促销费用投入多少万元时,厂家的利润最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某村庄拟修建一个无盖的圆柱形蓄水池(不计厚度).设该蓄水池的底面半径为r米,高为h米,体积为V立方米.假设建造成本仅与表面积有关,侧面的建造成本为100元/平方米,底面的建造成本为160元/平方米,该蓄水池的总建造成本为12 000π元(π为圆周率).
(1)将V表示成r的函数V(r),并求该函数的定义域;
(2)讨论函数V(r)的单调性,并确定r和h为何值时该蓄水池的体积最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a>b>1,若logab+logba= ![]() ,ab=ba , 则由a,b,3b,b2 , a﹣2b构成的包含元素最多的集合的子集个数是( )
,ab=ba , 则由a,b,3b,b2 , a﹣2b构成的包含元素最多的集合的子集个数是( )
A.32
B.16
C.8
D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com