
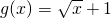 ,函数
,函数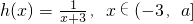 ,其中a为常数且a>0,令函数f(x)=g(x)•h(x).
,其中a为常数且a>0,令函数f(x)=g(x)•h(x). 时,求函数f(x)的值域;
时,求函数f(x)的值域; ?若存在,试写出所有满足条件的自然数a所构成的集合;若不存在,试说明理由.
?若存在,试写出所有满足条件的自然数a所构成的集合;若不存在,试说明理由. ,其定义域为[0,a];(2分)
,其定义域为[0,a];(2分)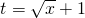 ,则
,则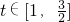 且x=(t-1)2
且x=(t-1)2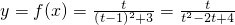 (5分)
(5分)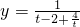
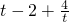 在[1,2]上递减,在[2,+∞)上递增,
在[1,2]上递减,在[2,+∞)上递增,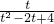 在
在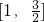 上递增,即此时f(x)的值域为
上递增,即此时f(x)的值域为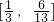 (8分)
(8分)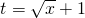 ,则
,则 且x=(t-1)2∴
且x=(t-1)2∴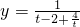
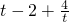 在[1,2]上递减,在[2,+∞)上递增,
在[1,2]上递减,在[2,+∞)上递增,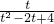 在[1,2]上递增,
在[1,2]上递增,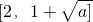 上递减,(10分)
上递减,(10分)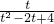 的最大值为
的最大值为 ,(11分)
,(11分)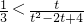
 ,由
,由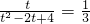 ,解得:t=1或t=4(12分)
,解得:t=1或t=4(12分) 时,
时, (13分)
(13分) 时,函数f(x)的定义域即可确定,利用换元和基本不等式求最值即可;
时,函数f(x)的定义域即可确定,利用换元和基本不等式求最值即可;

科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2011-2012学年江苏省无锡市惠山区洛社高中高三(上)9月段考数学试卷(解析版) 题型:解答题
 ,函数
,函数 ,其中a为常数且a>0,令函数f(x)=g(x)•h(x).
,其中a为常数且a>0,令函数f(x)=g(x)•h(x). 时,求函数f(x)的值域;
时,求函数f(x)的值域; ?若存在,试写出所有满足条件的自然数a所构成的集合;若不存在,试说明理由.
?若存在,试写出所有满足条件的自然数a所构成的集合;若不存在,试说明理由.查看答案和解析>>
科目:高中数学 来源:2006年上海市普陀区高考数学一模试卷(解析版) 题型:解答题
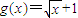 ,函数
,函数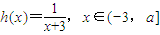 ,其中a为常数且a>0,令函数f(x)=g(x)•h(x).
,其中a为常数且a>0,令函数f(x)=g(x)•h(x).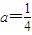 时,求函数f(x)的值域;
时,求函数f(x)的值域;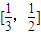 ?若存在,试写出所有满足条件的自然数a所构成的集合;若不存在,试说明理由.
?若存在,试写出所有满足条件的自然数a所构成的集合;若不存在,试说明理由.查看答案和解析>>
科目:高中数学 来源:2009年江苏省泰州市中学高三数学单元练习(一)(10月份)(解析版) 题型:解答题
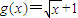 ,函数
,函数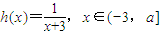 ,其中a为常数且a>0,令函数f(x)=g(x)•h(x).
,其中a为常数且a>0,令函数f(x)=g(x)•h(x).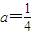 时,求函数f(x)的值域;
时,求函数f(x)的值域;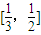 ?若存在,试写出所有满足条件的自然数a所构成的集合;若不存在,试说明理由.
?若存在,试写出所有满足条件的自然数a所构成的集合;若不存在,试说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com