
【题目】已知函数![]() 若对任意的实数x1,x2,x3,不等式f(x1)+f(x2)>f(x3)恒成立,则实数m的取值范围是( )
若对任意的实数x1,x2,x3,不等式f(x1)+f(x2)>f(x3)恒成立,则实数m的取值范围是( )
A.[1,4)B.(1,4)C.(![]() )D.[
)D.[![]() ]
]
科目:高中数学 来源: 题型:
【题目】有限数列![]() 同时满足下列两个条件:
同时满足下列两个条件:
①对于任意的![]() (
(![]() ),
),![]() ;
;
②对于任意的![]() (
(![]() ),
),![]() ,
,![]() ,
,![]() 三个数中至少有一个数是数列
三个数中至少有一个数是数列![]() 中的项.[来
中的项.[来
(1)若![]() ,且
,且![]() ,
,![]() ,
,![]() ,
,![]() ,求
,求![]() 的值;
的值;
(2)证明:![]() 不可能是数列
不可能是数列![]() 中的项;
中的项;
(3)求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,圆O的直径AB=6,C为圆周上一点,BC=3,平面PAC垂直圆O所在平面,直线PC与圆O所在平面所成角为60°,PA⊥PC.
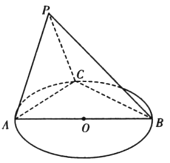
(1)证明:AP⊥平面PBC
(2)求二面角P—AB一C的余弦值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 在椭圆
在椭圆![]() 上,直线
上,直线![]() 与x,y轴分别交于A,B两点,0为坐标原点,且△OAB 的面积的最小值为
与x,y轴分别交于A,B两点,0为坐标原点,且△OAB 的面积的最小值为![]()

(1)求椭圆![]() 的离心率;
的离心率;
(2) 设点C、D、F2分别为椭圆![]() 的上、下顶点以及右焦点,E 为线段OD 的中点,直线F2E 与椭圆
的上、下顶点以及右焦点,E 为线段OD 的中点,直线F2E 与椭圆![]() 相交于M、N 两点,若
相交于M、N 两点,若![]() ,求椭圆
,求椭圆![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线Cn:x2﹣2nx+y2=0,(n=1,2,…).从点P(﹣1,0)向曲线Cn引斜率为kn(kn>0)的切线ln,切点为Pn(xn,yn).
(1)求数列{xn}与{yn}的通项公式;
(2)证明: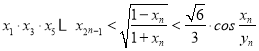 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的长轴长为4,左、右顶点分别为
的长轴长为4,左、右顶点分别为![]() ,经过点
,经过点![]() 的动直线与椭圆
的动直线与椭圆![]() 相交于不同的两点
相交于不同的两点![]() (不与点
(不与点![]() 重合).
重合).
(1)求椭圆![]() 的方程及离心率;
的方程及离心率;
(2)求四边形![]() 面积的最大值;
面积的最大值;
(3)若直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,判断点
,判断点![]() 是否位于一条定直线上?若是,写出该直线的方程. (结论不要求证明)
是否位于一条定直线上?若是,写出该直线的方程. (结论不要求证明)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国南宋数学家杨辉1261年所著的《详解九章算法》一书里出现了如图所示的表,即杨辉三角,这是数学史上的一个伟大成就,在“杨辉三角”中,第![]() 行的所有数字之和为
行的所有数字之和为![]() ,若去除所有为1的项,依次构成数列2,3,3,4,6,4,5,10,10,5,…,则此数列的前15项和为( )
,若去除所有为1的项,依次构成数列2,3,3,4,6,4,5,10,10,5,…,则此数列的前15项和为( )
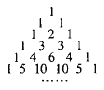
A. 110B. 114C. 124D. 125
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com