
【题目】已知函数![]() ,
, ![]() .
.
(Ⅰ)若函数![]() 为定义域上的单调函数,求实数
为定义域上的单调函数,求实数![]() 的取值范围;
的取值范围;
(Ⅱ)当![]() 时,函数
时,函数![]() 的两个极值点为
的两个极值点为![]() ,
, ![]() ,且
,且![]() .证明:
.证明: ![]() .
.
【答案】(1)![]() (2)详见解析。
(2)详见解析。
【解析】试题分析:(Ⅰ)首先求得函数的定义域与导函数,然后结合判别式判断导函数的符号,得到函数的单调性,从而求得![]() 的取值范围;(Ⅱ)首先将问题转化为
的取值范围;(Ⅱ)首先将问题转化为![]() 有两个不等的实根
有两个不等的实根![]() ,
, ![]() ,由此得到
,由此得到![]() 的范围,从而得到
的范围,从而得到![]() 的范围,然后根据
的范围,然后根据![]() 的表达式构造新函数,由此通过求导研究新函数的单调性使问题得证.
的表达式构造新函数,由此通过求导研究新函数的单调性使问题得证.
(Ⅰ)函数![]() 的定义域为
的定义域为![]() .
.
由题意![]()
![]() ,
, ![]() ,
, ![]() .
.
①若![]() ,即
,即![]() ,则
,则![]() 恒成立,则
恒成立,则![]() 在
在![]() 上为单调减函数;
上为单调减函数;
②若![]() ,即
,即![]() ,方程
,方程![]() 的两个根为
的两个根为![]() ,
, ![]() ,当
,当![]() 时,
时, ![]() ,所以函数
,所以函数![]() 单调递减,当
单调递减,当![]() 时,
时, ![]() ,所以函数
,所以函数![]() 单调递增,不符合题意.
单调递增,不符合题意.
综上,若函数![]() 为定义域上的单调函数,则实数
为定义域上的单调函数,则实数![]() 的取值范围为
的取值范围为![]() .
.
(Ⅱ)因为函数![]() 有两个极值点,所以
有两个极值点,所以![]() 在
在![]() 上有两个不等的实根,
上有两个不等的实根,
即![]() 有两个不等的实根
有两个不等的实根![]() ,
, ![]() ,
,
可得![]() ,且
,且![]() ,
,
因为![]() ,则
,则![]() ,可得
,可得![]() .
.
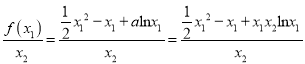
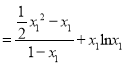 ,
,
![]() .
.
令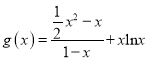 ,
, 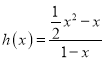 ,
, ![]() ,
,
∵![]() ,
,
又![]() ,
, ![]() 时,
时, ![]() ,
,
而![]() ,故
,故![]() 在
在![]() 上恒成立,
上恒成立,
所以![]() 在
在![]() 上恒成立,
上恒成立,
即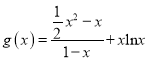 在
在![]() 上单调递减,
上单调递减,
所以![]() ,得证.
,得证.


科目:高中数学 来源: 题型:
【题目】公元263年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形的面积可无限接近圆的面积,并创立了“割圆术”,利用“割圆术”,刘徽得到了圆周率精确到小数点后两位的近似值3.14,这就是著名的“徽率”,利用刘徽的“割圆术”思想设计的一个程序框图,则输出的值为( )
(参考数据: ![]() )
)
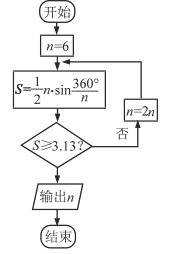
A. 12 B. 24 C. 48 D. 96
查看答案和解析>>
科目:高中数学 来源: 题型:
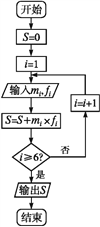
【题目】“世界睡眠日”定在每年的3月21日,某网站于2017年3月14日到3月20日持续一周网上调查公众日平均睡眠的时间(单位:小时),共有2 000人参加调查,现将数据整理分组后如下表所示.
序号(i) | 分组睡眠时间 | 组中值(mi) | 频数(人数) | 频率(fi) |
1 | [4,5) | 4.5 | 80 | |
2 | [5,6) | 5.5 | 520 | 0.26 |
3 | [6,7) | 6.5 | 600 | 0.30 |
4 | [7,8) | 7.5 | ||
5 | [8,9) | 8.5 | 200 | 0.10 |
6 | [9,10] | 9.5 | 40 | 0.02 |
(1)求出表中空白处的数据,并将表格补充完整.
(2)画出频率分布直方图.
(3)为了对数据进行分析,采用了计算机辅助计算.程序框图如图所示,求输出的S值,并说明S的统计意义.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某港口有一个泊位,现统计了某月100艘轮船在该泊位停靠的时间(单位:小时),如果停靠时间不足半小时按半小时计时,超过半小时不足1小时按1小时计时,以此类推,统计结果如表:
停靠时间 | 2.5 | 3 | 3.5 | 4 | 4.5 | 5 | 5.5 | 6 |
轮船数量 | 12 | 12 | 17 | 20 | 15 | 13 | 8 | 3 |
(Ⅰ)设该月100艘轮船在该泊位的平均停靠时间为![]() 小时,求
小时,求![]() 的值;
的值;
(Ⅱ)假定某天只有甲、乙两艘轮船需要在该泊位停靠![]() 小时,且在一昼夜的时间段中随机到达,求这两艘轮船中至少有一艘在停靠该泊位时必须等待的概率.
小时,且在一昼夜的时间段中随机到达,求这两艘轮船中至少有一艘在停靠该泊位时必须等待的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将7名应届师范大学毕业生分配到3所中学任教.
(1)4个人分到甲学校,2个人分到乙学校,1个人分到丙学校,有多少种不同的分配方案?
(2)一所学校去4个人,另一所学校去2个人,剩下的一个学校去1个人,有多少种不同的分配方案?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的右焦点为
的右焦点为![]() ,右顶点为
,右顶点为![]() ,设离心率为
,设离心率为![]() ,且满足
,且满足![]() ,其中
,其中![]() 为坐标原点.
为坐标原点.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)过点(0,1)的直线![]() 与椭圆交于
与椭圆交于![]() ,
,![]() 两点,求
两点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为调查高三年级学生的身高情况,按随机抽样的方法抽取80名学生,得到男生身高情况的频率分布直方图(图1)和女生身高情况的频率分布直方图(图2).已知图1中身高在170~175cm的男生人数有16人.

(1)根据频率分布直方图,完成下列的![]() 列联表,并判断能有多大(百分几)的把握认为“身高与性别有关”?
列联表,并判断能有多大(百分几)的把握认为“身高与性别有关”?
|
| 总计 | |
男生身高 | |||
女神身高 | |||
总计 |
(2)在上述80名学生中,从身高在170-175cm之间的学生按男、女性别分层抽样的方法,抽出5人,从这5人中选派3人当旗手,求3人中恰好有一名女生的概率.
参考公式: 
参考数据:
| 0.025 | 0.610 | 0.005 | 0.001 |
| 5.024 | 4.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com