
【题目】已知函数![]()
![]() .
.
(1)讨论![]() 的单调性;
的单调性;
(2)若![]() 在区间
在区间![]() 上有两个零点,求
上有两个零点,求![]() 的取值范围.
的取值范围.
【答案】(1)详解见解析;(2)![]()
【解析】试题分析:
(1)首先求得函数的导函数,然后分类讨论求得函数的单调区间即可;
(2)结合(1)的结论,利用导函数与原函数的关系整理可得![]() 的取值范围是
的取值范围是![]() .
.
试题解析:
(1)![]() 的定义域为
的定义域为![]() ,
,![]() ,
,
令![]() 可得
可得![]() 或
或![]() .下面分三种情况.
.下面分三种情况.
![]() 当
当![]() 时,可得
时,可得![]() ,由
,由![]() 得
得![]() ,由
,由![]() 得
得![]() ,
,
此时![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() .
.
![]() 当
当![]() 时,由
时,由![]() 得
得![]() 或
或![]() ,由
,由![]() 得
得![]() ,
,
此时![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() .
.
![]() 当
当![]() 时,
时,![]() ,
,![]() 在区间
在区间![]() 上单调递增.
上单调递增.
由(1)得,当![]() 时,
时,![]() 在
在![]() 处取得最小值
处取得最小值![]() ,且
,且![]() 在区间
在区间![]() 内先减后增,又
内先减后增,又![]() ,
,
![]() ,要使得
,要使得![]() 在区间
在区间![]() 上有两个零点,
上有两个零点,
必须有![]() 且
且![]() ,由此可得
,由此可得![]() .
.
当![]() 时,
时,![]() ,显然
,显然![]() 在区间
在区间![]() 上不存在两个零点.
上不存在两个零点.
当![]() 时,由(1)得
时,由(1)得![]() 在区间
在区间![]() 内先减后增,
内先减后增,
又![]() ,
,![]() ,
,
故此时![]() 在区间
在区间![]() 上不存在两个零点.
上不存在两个零点.
当![]() 时,由(1)得
时,由(1)得![]() 在区间
在区间![]() 内先增,先减,后增.
内先增,先减,后增.
又![]() ,
,![]() ,
,
故此时![]() 在区间
在区间![]() 上不存在两个零点.
上不存在两个零点.
当![]() 时,由(1)得
时,由(1)得![]() 在区间
在区间![]() 上单调递增,
上单调递增,
![]() 在区间
在区间![]() 上不存在两个零点.
上不存在两个零点.
综上,![]() 的取值范围是
的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,是一块足球训练场地,其中球门AB宽7米,B点位置的门柱距离边线EF的长为21米,现在有一球员在该训练场地进行直线跑动中的射门训练.球员从离底线AF距离x(x≥10)米,离边线EF距离a(7≤a≤14)米的C处开始跑动,跑动线路为CD(CD∥EF),设射门角度∠ACB=θ. 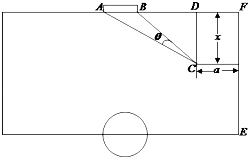
(1)若a=14,
①当球员离底线的距离x=14时,求tanθ的值;
②问球员离底线的距离为多少时,射门角度θ最大?
(2)若tanθ= ![]() ,当a变化时,求x的取值范围.
,当a变化时,求x的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】参加衡水中学数学选修课的同学,对某公司的一种产品销量与价格进行统计,得到如下数据和散点图:
定价 |
|
|
|
|
|
|
年销售 |
|
|
|
|
|
|
|
|
|
|
|
|
|
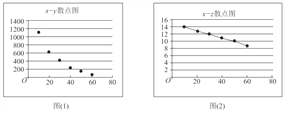
(参考数据:![]()
![]() )
)
(I)根据散点图判断,![]() 与
与![]() ,
,![]() 与
与![]() 哪一对具有较强的线性相关性(给出判断即可,不必说明理由)?
哪一对具有较强的线性相关性(给出判断即可,不必说明理由)?
(II)根据(I)的判断结果有数据,建立![]() 关于
关于![]() 的回归方程(方程中的系数均保留两位有效数字);
的回归方程(方程中的系数均保留两位有效数字);
(III)定价为多少元/![]() 时,年利润的预报值最大?
时,年利润的预报值最大?
附:对一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: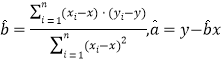 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某搜索引擎广告按照付费价格对搜索结果进行排名,点击一次付费价格排名越靠前,被点击的次数也可能会提高,已知某关键词被甲、乙等多个公司竞争,其中甲、乙付费情况与每小时点击量结果绘制成如下的折线图.

(1)试根据所给数据计算每小时点击次数的均值方差并分析两组数据的特征;
(2)若把乙公司设置的每次点击价格为x,每小时点击次数为![]() ,则点
,则点![]() 近似在一条直线附近.试根据前5次价格与每小时点击次数的关系,求y关于x的回归直线
近似在一条直线附近.试根据前5次价格与每小时点击次数的关系,求y关于x的回归直线![]() .(附:回归方程系数公式:
.(附:回归方程系数公式: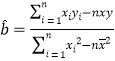 ,
,![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】政府鼓励创新、创业,银行给予低息贷款.一位大学毕业生向自主创业,经过市场调研、测算,有两个方案可供选择.
方案1:开设一个科技小微企业,需要一次性贷款40万元,第一年获利是贷款额的10%,以后每年比上一年增加25%的利润.
方案2:开设一家食品小店,需要一次性贷款20万元,第一年获利是贷款额的15%,以后每年比上一年增加利润1.5万元.两种方案使用期限都是10年,到期一次性还本付息.两种方案均按年息2%的复利计算(参考数据:1.259=7.45,1.2510=9.3,1.029=1.20,1.0210=1.22).
(1)10年后,方案1,方案2的总收入分别有多少万元?
(2)10年后,哪一种方案的利润较大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线的方程为![]() ,过点
,过点![]() 的一条直线与抛物线
的一条直线与抛物线![]() 交于
交于![]() 两点,若抛物线在
两点,若抛物线在![]() 两点的切线交于点
两点的切线交于点![]() .
.
(1)求点![]() 的轨迹方程;
的轨迹方程;
(2)设直线![]() 与直线
与直线![]() 的夹角为
的夹角为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知点A(2,4),直线l:x﹣2y+1=0.
(1)求过点A且平行于l的直线的方程;
(2)若点M在直线l上,且AM⊥l,求点M的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com