
分析 (1)化函数f(x)为正弦型函数,求出$x∈[0,\frac{π}{2}]$时f(x)的取值范围即可;
(2)根据复合函数的单调性列出不等式组,求出x的取值范围即可.
解答 解:(1)函数$f(x)=2{sin^2}(x+\frac{3π}{2})+\sqrt{3}$sin(π-2x)
=2cos2x+$\sqrt{3}$sin2x
=cos2x+$\sqrt{3}$sin2x+1
=2sin(2x+$\frac{π}{6}$)+1,
当$x∈[0,\frac{π}{2}]$时,$\frac{π}{6}≤2x+\frac{π}{6}≤\frac{7π}{6}$,
故$-\frac{1}{2}≤sin(2x+\frac{π}{6})≤1$,
$0≤2sin(2x+\frac{π}{6})+1≤3$,
所以f(x)的取值范围是[0,3];
(2)由题意有$\left\{\begin{array}{l}{2sin(2x+\frac{π}{6})+1>0}\\{\frac{π}{2}+2kπ≤2x+\frac{π}{6}≤\frac{3π}{2}+2kπ,k∈Z}\end{array}\right.$,
解得$\left\{\begin{array}{l}{-\frac{π}{6}+2kπ<2x+\frac{π}{6}<\frac{7π}{6}+2kπ,k∈Z}\\{\frac{π}{2}+2kπ≤2x+\frac{π}{6}≤\frac{3π}{2}+2kπ,k∈Z}\end{array}\right.$,
即$\frac{π}{2}$+2kπ≤2x+$\frac{π}{6}$<$\frac{7π}{6}$+2kπ,k∈Z,
所以$\frac{π}{6}$+kπ≤x<$\frac{π}{2}$+kπ,k∈Z;
所以函数$y={log_{\frac{1}{2}}}f(x)$的单调增区间为[$\frac{π}{6}$+kπ,$\frac{π}{2}$+kπ),k∈Z.
点评 本题考查了三角函数的化简与三角函数的图象与性质的应用问题,是基础题目.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| 16 | 22 | 77 | 94 | 39 | 49 | 54 | 43 | 54 | 82 | 17 | 37 | 93 | 23 | 78 | 87 | 35 | 20 | 96 | 43 |
| 84 | 42 | 17 | 53 | 31 | 57 | 24 | 55 | 06 | 88 | 77 | 04 | 74 | 47 | 67 | 21 | 76 | 33 | 50 | 25 |
| A. | 23 | B. | 37 | C. | 35 | D. | 17 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{\sqrt{7}}{3}$] | B. | (0,$\frac{\sqrt{5}}{2}$] | C. | ($\sqrt{2}$,$\frac{5}{3}$] | D. | ($\sqrt{2}$,$\frac{\sqrt{13}}{3}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | n<m | B. | n>m | C. | n=m | D. | 不能确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$ | B. | $\frac{5}{9}$ | C. | $\frac{7}{9}$ | D. | $\frac{5}{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
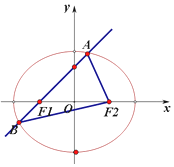 如图,已知中心在坐标原点的椭圆C,F1,F2 分别为椭圆的左、右焦点,右顶点到右准线的距离为2,离心率为$\frac{1}{2}$.过椭圆的左焦点F1 任意作一条直线l 与椭圆交于A,B 两点.设A(x1,y1),B(x2,y2).
如图,已知中心在坐标原点的椭圆C,F1,F2 分别为椭圆的左、右焦点,右顶点到右准线的距离为2,离心率为$\frac{1}{2}$.过椭圆的左焦点F1 任意作一条直线l 与椭圆交于A,B 两点.设A(x1,y1),B(x2,y2).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{2}$ | B. | $-\frac{{\sqrt{3}}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
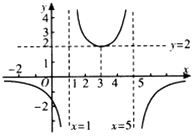
| A. | 1:6:5:(-8) | B. | 1:6:5:8 | C. | 1:(-6):5:8 | D. | 1:(-6):5:(-8) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com