
【题目】已知椭圆C:![]() 过点M(2,3),点A为其左顶点,且AM的斜率为
过点M(2,3),点A为其左顶点,且AM的斜率为![]() ,
,
(1)求C的方程;
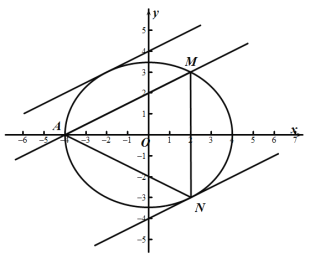
(2)点N为椭圆上任意一点,求△AMN的面积的最大值.
【答案】(1)![]() ;(2)12.
;(2)12.
【解析】
(1)由题意分别求得a,b的值即可确定椭圆方程;
(2)首先利用几何关系找到三角形面积最大时点N的位置,然后联立直线方程与椭圆方程,结合判别式确定点N到直线AM的距离即可求得三角形面积的最大值.
(1)由题意可知直线AM的方程为:![]() ,即
,即![]() .
.
当y=0时,解得![]() ,所以a=4,
,所以a=4,
椭圆![]() 过点M(2,3),可得
过点M(2,3),可得![]() ,
,
解得b2=12.
所以C的方程:![]() .
.
(2)设与直线AM平行的直线方程为:![]() ,
,
如图所示,当直线与椭圆相切时,与AM距离比较远的直线与椭圆的切点为N,此时△AMN的面积取得最大值.
联立直线方程![]() 与椭圆方程
与椭圆方程![]() ,
,
可得:![]() ,
,
化简可得:![]() ,
,
所以![]() ,即m2=64,解得m=±8,
,即m2=64,解得m=±8,
与AM距离比较远的直线方程:![]() ,
,
直线AM方程为:![]() ,
,
点N到直线AM的距离即两平行线之间的距离,
利用平行线之间的距离公式可得:![]() ,
,
由两点之间距离公式可得![]() .
.
所以△AMN的面积的最大值:![]() .
.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:高中数学 来源: 题型:
【题目】某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费![]() (单位:千元)对年销售量y(单位:t)和年利润z(单位:千元)的影响,对近8年的年宣传费
(单位:千元)对年销售量y(单位:t)和年利润z(单位:千元)的影响,对近8年的年宣传费![]() 和年销售量
和年销售量![]() (
(![]() )数据作了初步处理,得到下面的散点图及一些统计量的值.
)数据作了初步处理,得到下面的散点图及一些统计量的值.

|
|
|
|
|
|
|
46.6 | 563 | 6.8 | 289.8 | 1.6 | 1.469 | 108.8 |
表中![]() ,
,![]()
(1)根据散点图判断,![]() 与
与![]() 哪一个适宜作为年销售量y关于年宣传费x的回归方类型?给出判断即可,不必说明理由
哪一个适宜作为年销售量y关于年宣传费x的回归方类型?给出判断即可,不必说明理由
(2)根据(1)的判断结果及表中数据,建立y关于x的回归方程;
(3)已知这种产品的年利润z与x、y的关系为![]() 根据(2)的结果回答下列问题:
根据(2)的结果回答下列问题:
①年宣传费![]() 时,年销售量及年利润的预报值是多少?
时,年销售量及年利润的预报值是多少?
②年宣传费x为何值时,年利润的预报值最大?
附:对于一组数据![]() ,其回归线
,其回归线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,以坐标原点为极点,
中,以坐标原点为极点,![]() 轴非负半轴为极轴建立极坐标系,已知直线
轴非负半轴为极轴建立极坐标系,已知直线![]() 的极坐标方程为
的极坐标方程为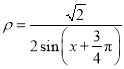 ,曲线
,曲线![]() 的参数方程为
的参数方程为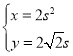 (
(![]() 为参数).
为参数).
(1)若直线![]() 平行于直线
平行于直线![]() ,且与曲线
,且与曲线![]() 只有一个公共点,求直线
只有一个公共点,求直线![]() 的方程;
的方程;
(2)若直线![]() 与曲线
与曲线![]() 交于两点
交于两点![]() ,
,![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学的学生积极参加体育锻炼,其中有96%的学生喜欢足球或游泳,60%的学生喜欢足球,82%的学生喜欢游泳,则该中学既喜欢足球又喜欢游泳的学生数占该校学生总数的比例是( )
A.62%B.56%
C.46%D.42%
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知极坐标系的极点在平面直角坐标系的原点![]() 处,极轴与
处,极轴与![]() 轴的正半轴重合,且长度单位相同;曲线
轴的正半轴重合,且长度单位相同;曲线![]() 的方程是
的方程是![]() ,直线
,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() ),设
),设![]() , 直线
, 直线![]() 与曲线
与曲线![]() 交于
交于 ![]() 两点.
两点.
(1)当![]() 时,求
时,求![]() 的长度;
的长度;
(2)求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某种气垫船的最大航速是![]() 海里小时,船每小时使用的燃料费用和船速的平方成正比.若船速为
海里小时,船每小时使用的燃料费用和船速的平方成正比.若船速为![]() 海里小时,则船每小时的燃料费用为
海里小时,则船每小时的燃料费用为![]() 元,其余费用(不论船速为多少)都是每小时
元,其余费用(不论船速为多少)都是每小时![]() 元。甲乙两地相距
元。甲乙两地相距![]() 海里,船从甲地匀速航行到乙地.
海里,船从甲地匀速航行到乙地.
(1)试把船从甲地到乙地所需的总费用![]() ,表示为船速
,表示为船速![]() (海里小时)的函数,并指出函数的定义域;
(海里小时)的函数,并指出函数的定义域;
(2)当船速为每小时多少海里时,船从甲地到乙地所需的总费用最少?最少费用为多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 有两个不同零点
有两个不同零点![]() 、
、![]() (
(![]() ),设函数
),设函数![]() 的定义域为
的定义域为![]() ,且
,且![]() 的最大值记为
的最大值记为![]() ,最小值记为
,最小值记为![]() .
.
(1)求![]() (用
(用![]() 表示);
表示);
(2)当![]() 时,试问以
时,试问以![]() 、
、![]() 、
、![]() 为长度的线段能否组成一个三角形,如果不一定,进一步求出
为长度的线段能否组成一个三角形,如果不一定,进一步求出![]() 的取值范围,使它们能组成一个三角形;
的取值范围,使它们能组成一个三角形;
(3)求![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com