
【题目】函数f(x)=﹣x2+(3﹣2m)x+2+m(0<m≤1).
(1)若x∈[0,m],证明:f(x)≤ ![]() ;
;
(2)求|f(x)|在[﹣1,1]上的最大值g(m).
【答案】
(1)证明:∵0<m≤1,∴f(x)的对称轴x= ![]() ∈[
∈[ ![]() ,
, ![]() ),
),
①0<m≤ ![]() 时,函数f(x)=﹣x2+(3﹣2m)x+2+m开口向下,在[0,m)函数是增函数,
时,函数f(x)=﹣x2+(3﹣2m)x+2+m开口向下,在[0,m)函数是增函数,
∴f(x)≤f(m)=﹣m2+(3﹣2m)m+2+m=﹣3m2+4m+2=﹣3 ![]() ;
;
②当 ![]() 时,f(x)max=f(
时,f(x)max=f( ![]() )=
)= ![]() =
= ![]() <
< ![]()
![]() .
.
综上,f(x)≤ ![]() ;
;
(2)解:函数f(x)=﹣x2+(3﹣2m)x+2+m=﹣(x﹣ ![]() )2+
)2+ ![]() ,
,
若0 ![]() ,则0<2m≤1,f(x)的对称轴x=
,则0<2m≤1,f(x)的对称轴x= ![]() ∈[1,
∈[1, ![]() ),
),
则f(x)在[﹣1,1]上为增函数,
∵f(1)=4﹣m∈[ ![]() ),|f(﹣1)|=|3m﹣2|∈[
),|f(﹣1)|=|3m﹣2|∈[ ![]() ,2).
,2).
∴|f(1)|>|f(﹣1)|,
∴|f(x)|在[﹣1,1]上的最大值g(m)=f(1)=4﹣m;
若 ![]() <m≤1,则1<2m≤2,f(x)的对称轴x=
<m≤1,则1<2m≤2,f(x)的对称轴x= ![]() ∈(
∈( ![]() ,1],
,1],
则f(x)在[﹣1,1]上先增后减,且最小值为f(﹣1)=3m﹣2,最大值为f( ![]() )=m2﹣2m+
)=m2﹣2m+ ![]() .
.
∵|f(﹣1)|=|3m﹣2|∈[0,1],f( ![]() )=m2﹣2m+
)=m2﹣2m+ ![]() =
= ![]() .
.
∴|f(x)|在[﹣1,1]上的最大值g(m)=f( ![]() )=m2﹣2m+
)=m2﹣2m+ ![]() .
.
综上,g(m)= 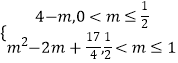
【解析】(1)求出二次函数的对称轴方程,由m的范围分类可得二次函数在[0,m]上的单调性,得到二次函数的最大值,由配方法证明f(x)≤ ![]() ;(2)分0
;(2)分0 ![]() 和
和 ![]() <m≤1两种情况求出函数f(x)在[﹣1,1]上的最值,再由最值的绝对值的大小求得|f(x)|在[﹣1,1]上的最大值g(m).
<m≤1两种情况求出函数f(x)在[﹣1,1]上的最值,再由最值的绝对值的大小求得|f(x)|在[﹣1,1]上的最大值g(m).
【考点精析】利用二次函数的性质对题目进行判断即可得到答案,需要熟知当![]() 时,抛物线开口向上,函数在
时,抛物线开口向上,函数在![]() 上递减,在
上递减,在![]() 上递增;当
上递增;当![]() 时,抛物线开口向下,函数在
时,抛物线开口向下,函数在![]() 上递增,在
上递增,在![]() 上递减.
上递减.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】函数f(x)= ![]() 是定义在区间(﹣1,1)上的奇函数,且f(2)=
是定义在区间(﹣1,1)上的奇函数,且f(2)= ![]() ,
,
(1)确定函数f(x)的解析式;
(2)用定义法证明f(x)在区间(﹣1,1)上是增函数;
(3)解不等式f(t﹣1)+f(t)<0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2017省息一中第七次适应性考】已知函数![]() (
(![]() ),且
),且![]() 的导数为
的导数为![]() .
.
(Ⅰ)若![]() 是定义域内的增函数,求实数
是定义域内的增函数,求实数![]() 的取值范围;
的取值范围;
(Ⅱ)若方程![]() 有3个不同的实数根,求实数
有3个不同的实数根,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合A={x|ax2+bx+1=0}(a∈R,b∈R),集合B={﹣1,1}.
(1)若BA,求实数a的值;
(2)若A∩B≠,求a2﹣b2+2a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|x2﹣3x<0},B={x|(x+2)(4﹣x)≥0},C={x|a<x≤a+1}.
(1)求A∩B;
(2)若B∪C=B,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】假设关于某设备使用年限x(年)和所支出的维修费用y(万元)有如下统计资料:
2 | 3 | 4 | 5 | 6 | |
y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
若由资料知,y对x呈线性相关关系,试求:
(Ⅰ)请画出上表数据的散点图;
(Ⅱ)请根据上表提供的数据,求出y关于x的线性回归方程![]() =bx+
=bx+![]() ;
;
(Ⅲ)估计使用年限为10年时,维修费用约是多少?
(参考数据:2×2.2+3×3.8+4×5.5+5×6.5+6×7.0=112.3)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2+bx+c(a,b,c∈R,a≠0),对任意的x∈R,都有f(x﹣4)=f(2﹣x)成立,
(1)求2a﹣b的值;
(2)函数f(x)取得最小值0,且对任意x∈R,不等式x≤f(x)≤( ![]() )2恒成立,求函数f(x)的解析式;
)2恒成立,求函数f(x)的解析式;
(3)若方程f(x)=x没有实数根,判断方程f(f(x))=x根的情况,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com