
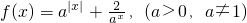
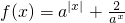 =3
=3 ,g(x)=a-x+2ax
,g(x)=a-x+2ax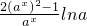
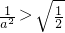 即
即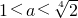 时,对?x∈(-2,0),g'(x)>0,
时,对?x∈(-2,0),g'(x)>0,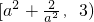 ,由此g(x)有最小值
,由此g(x)有最小值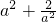 与a有关,不符合.
与a有关,不符合.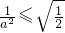 即
即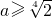 时,由g'(x)=0得
时,由g'(x)=0得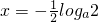
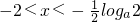 时,g'(x)<0;
时,g'(x)<0;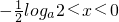 时,g'(x)>0
时,g'(x)>0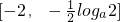 上递减,在
上递减,在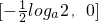 上递增,∴g(x)min=
上递增,∴g(x)min=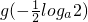 =
=
 与a无关,符合要求(6分)
与a无关,符合要求(6分)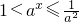 ,g(x)=a-x+2ax,
,g(x)=a-x+2ax,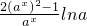 <0,∴g(x)在[-2,0)上递减,
<0,∴g(x)在[-2,0)上递减,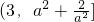 ,由此g(x)有最大值
,由此g(x)有最大值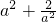 与a有关,不符合
与a有关,不符合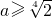 (6分).
(6分).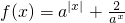 =3,对x的范围分类进行讨论求解即可.求解本题宜分为两类,分别为x≥0时与x<0时.
=3,对x的范围分类进行讨论求解即可.求解本题宜分为两类,分别为x≥0时与x<0时.

 科学实验活动册系列答案
科学实验活动册系列答案科目:高中数学 来源: 题型:
| 4x |
| x2+a |
| x | 0 | 0.1 | 0.2 | 0.5 | 0.8 | 1 | 1.2 | 1.5 | 1.8 | 2 | 4 | 6 | … |
| y | 0 | 0.396 | 0.769 | 1.6 | 1.951 | 2 | 1.967 | 1.846 | 1.698 | 1.6 | 0.941 | 0.649 | … |
| 4x |
| x2+a |
| 3 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a(x-1) |
| x+1 |
| m-n |
| lnm-lnn |
| m+n |
| 2 |
查看答案和解析>>
科目:高中数学 来源:2010年江苏省南通市海安高级中学高三5月自检数学试卷(1)(解析版) 题型:解答题

查看答案和解析>>
科目:高中数学 来源:2010年江苏省南通市如皋中学高三质量检测数学试卷(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com