
【题目】房屋的天花板上点![]() 处有一光源,
处有一光源,![]() 在地面上的射影为
在地面上的射影为![]() ,在地面上放置正棱锥
,在地面上放置正棱锥![]() ,底面
,底面![]() 接触地面.已知正四棱锥
接触地面.已知正四棱锥![]() 的高为
的高为![]() ,底面
,底面![]() 的边长为
的边长为![]() ,
,![]() 与正方形
与正方形![]() 的中心
的中心![]() 的距离为
的距离为![]() ,又
,又![]() 长为
长为![]() ,则棱锥影子(不包括底面
,则棱锥影子(不包括底面![]() )的面积的最大值为________.
)的面积的最大值为________.
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线C的参数方程为![]() (
(![]() 为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为
为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为![]() .
.
(1)求曲线C的极坐标方程和直线l的直角坐标方程;
(2)若射线![]() 与曲线C交于点A(不同于极点O),与直线l交于点B,求
与曲线C交于点A(不同于极点O),与直线l交于点B,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
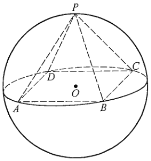
【题目】如图所示,正四棱锥![]() 底面的四个顶点
底面的四个顶点![]() ,
,![]() ,
,![]() ,
,![]() 在球
在球![]() 的同一个大圆上,点
的同一个大圆上,点![]() 在球面上,且已知
在球面上,且已知![]() .
.
(1)求球![]() 的表面积;
的表面积;
(2)设![]() 为
为![]() 中点,求异面直线
中点,求异面直线![]() 与
与![]() 所成角的大小.
所成角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】观察不等式:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 由此归纳第
由此归纳第![]() 个不等式为____________;要用数学归纳法证明该不等式,由
个不等式为____________;要用数学归纳法证明该不等式,由![]() 时不等式成立,推证
时不等式成立,推证![]() 时,左边应增加的项数为____________.
时,左边应增加的项数为____________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:![]() 的焦点为F,直线y=4与y轴的交点为P,与C的交点为Q,且
的焦点为F,直线y=4与y轴的交点为P,与C的交点为Q,且![]() .
.
(1)求抛物线C的方程;
(2)过F的直线l与C相交于A,B两点,若AB的垂直平分线![]() 与C相交于M,N两点,且A,M,B,N四点在同一个圆上,求直线l的方程.
与C相交于M,N两点,且A,M,B,N四点在同一个圆上,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,以等腰直角三角形斜边BC上的高AD为折痕,把△ABD与△ACD折成互相垂直的两个平面后,某学生得出下列四个结论:
①![]() ;
;
②∠BAC=60°;
③三棱锥D﹣ABC是正三棱锥;
④平面ADC的法向量和平面ABC的法向量互相垂直.
其中正确结论的序号是 .(请把正确结论的序号都填上)

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的首项
的首项![]() (
(![]() 是常数,且
是常数,且![]() ),
),![]()
![]() ,数列
,数列![]() 的首项
的首项![]() ,
,![]()
![]() .
.
(1)证明:![]() 从第2项起是以2为公比的等比数列;
从第2项起是以2为公比的等比数列;
(2)设![]() 为数列
为数列![]() 的前
的前![]() 项和,且
项和,且![]() 是等比数列,求实数
是等比数列,求实数![]() 的值;
的值;
(3)当![]() 时,求数列
时,求数列![]() 的最小项.
的最小项.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在气象台![]() 正南方向
正南方向![]() 处有一台风中心,它以
处有一台风中心,它以![]() 的速度向北偏东
的速度向北偏东![]() 方向移动,距台风中心
方向移动,距台风中心![]() 以内的地方都要受其影响.问:从现在起,大约多长时间后,气象台
以内的地方都要受其影响.问:从现在起,大约多长时间后,气象台![]() 所在地将遭受台风影响?持续多长时间?(
所在地将遭受台风影响?持续多长时间?(![]() ,
,![]() ,结果精确到0.01)
,结果精确到0.01)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com