
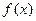 的定义域为
的定义域为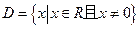 ,且满足对于任意的实数
,且满足对于任意的实数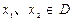 ,有
,有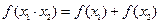 .
.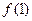 的值; (Ⅱ)判断
的值; (Ⅱ)判断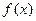 的奇偶性并证明;
的奇偶性并证明; II)若
II)若 ,且
,且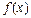 在
在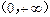 上是增函数,解关于
上是增函数,解关于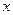 的不等式
的不等式 .
. 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com