
分析 (Ⅰ)由$f(x)=lg\frac{1+ax}{1-x}(a>0)$为奇函数得:f(-x)+f(x)=0,即可求a;
(Ⅱ)当b>1时,设 $h(x)=g(x)-ln|x|=\frac{2}{x^2}+b-ln|x|$,则h(x)是偶函数且在(0,+∞)上递减,即可讨论方徎g(x)=ln|x|实数根的个数;
(Ⅲ)不等式f(1-x)≤lgg(x)等价于$\frac{2-x}{x}≤\frac{2}{x^2}+b$,即$b≥-\frac{2}{x^2}+\frac{2}{x}-1$在$x∈[\frac{1}{3},\frac{1}{2}]$有解,故只需$b≥{(-\frac{2}{x^2}+\frac{2}{x}-1)_{min}}$,即可求b的取值范围.
解答 解:(Ⅰ)由$f(x)=lg\frac{1+ax}{1-x}(a>0)$为奇函数得:f(-x)+f(x)=0,
即$lg\frac{1-ax}{1+x}+lg\frac{1+ax}{1-x}=lg\frac{{1-{a^2}{x^2}}}{{1-{x^2}}}=0$,(2分)
所以$\frac{{1-{a^2}{x^2}}}{{1-{x^2}}}=1$,解得a=1,(4分)
(Ⅱ)当b>1时,设 $h(x)=g(x)-ln|x|=\frac{2}{x^2}+b-ln|x|$,
则h(x)是偶函数且在(0,+∞)上递减
又$h(1)=2+b>0,h({e^{2b}})=\frac{2}{{{e^{4b}}}}-b<0$
所以h(x)在(0,+∞)上有惟一的零点,方徎g(x)=ln|x|有2个实数根.…(8分)
(Ⅲ)不等式f(1-x)≤lgg(x)等价于$\frac{2-x}{x}≤\frac{2}{x^2}+b$,
即$b≥-\frac{2}{x^2}+\frac{2}{x}-1$在$x∈[\frac{1}{3},\frac{1}{2}]$有解,
故只需$b≥{(-\frac{2}{x^2}+\frac{2}{x}-1)_{min}}$,(10分)
因为$x∈[\frac{1}{3},\frac{1}{2}]$,所以$\frac{1}{x}∈[2,3]$,
函数$y=-2{(\frac{1}{x}-\frac{1}{2})^2}-\frac{1}{2}$,
所以${y_{min}}=-2{(3-\frac{1}{2})^2}-\frac{1}{2}=-13$,
所以b≥-13,所以b的取值范围是[-13,+∞).(12分)
点评 本题考查函数的奇偶性、单调性、考查有解问题,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | x=2或3x-4y+10=0 | B. | x=2或x+2y-10=0 | C. | y=4或3x-4y+10=0 | D. | y=4或x+2y-10=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
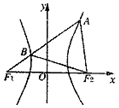 如图,F1、F2是双曲线$\frac{x^2}{9}-\frac{y^2}{b^2}=1(b>0)$的左、右焦点,过F1的直线l与双曲线分别交于点A、B,若△ABF2为等边三角形,则△BF1F2的面积为( )
如图,F1、F2是双曲线$\frac{x^2}{9}-\frac{y^2}{b^2}=1(b>0)$的左、右焦点,过F1的直线l与双曲线分别交于点A、B,若△ABF2为等边三角形,则△BF1F2的面积为( )| A. | $8\sqrt{3}$ | B. | $9\sqrt{3}$ | C. | $18\sqrt{3}$ | D. | $27\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某校100名学生期中考试数学成绩的频率分布直方图如图,其中成绩分组区间如下:
某校100名学生期中考试数学成绩的频率分布直方图如图,其中成绩分组区间如下:| 组号 | 第一组 | 第二组 | 第三组 | 第四组 | 第五组 |
| 分组 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
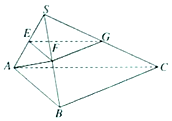 如图,在三棱锥S-ABC中,平面SAB⊥平面SBC,AB⊥BC,AS=AB,点E、F、G分别是棱SA、SB、SC的中点.求证:
如图,在三棱锥S-ABC中,平面SAB⊥平面SBC,AB⊥BC,AS=AB,点E、F、G分别是棱SA、SB、SC的中点.求证:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2lg5 | B. | 0 | C. | -1 | D. | -2lg5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com