
 将边长为1的正三角形ABC按如图所示的方式放置,其中顶点A与坐标原点重合.记边AB所在直线的倾斜角为θ,已知
将边长为1的正三角形ABC按如图所示的方式放置,其中顶点A与坐标原点重合.记边AB所在直线的倾斜角为θ,已知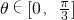 .
. 的坐标(要求将结果化简为形如(cosα,sinα)的形式);
的坐标(要求将结果化简为形如(cosα,sinα)的形式); ),sin(θ+
),sin(θ+ )),…(2分)
)),…(2分) =(cos(θ+
=(cos(θ+ )-cosθ,sin(θ+
)-cosθ,sin(θ+ )-sinθ),…(3分)
)-sinθ),…(3分) sinθ-
sinθ- cosθ,
cosθ, cosθ-
cosθ- sinθ)
sinθ) ),sin(θ+
),sin(θ+ )).…(7分)
)).…(7分) 到
到 (B移到A,C移到D),…(2分)
(B移到A,C移到D),…(2分) 的坐标与
的坐标与 的坐标相等,都等于点D的坐标.…(3分)
的坐标相等,都等于点D的坐标.…(3分) +θ,
+θ,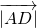 =1,
=1, ),sin(θ+
),sin(θ+ )),
)), =(cos(θ+
=(cos(θ+ ),sin(θ+
),sin(θ+ )).…(7分)
)).…(7分) )|+|sin(θ+
)|+|sin(θ+ ))|,…(8分)
))|,…(8分) ],
], ∈[
∈[ ,π],…(9分)
,π],…(9分) )+sin(θ+
)+sin(θ+ )…(11分)
)…(11分) sin(θ+
sin(θ+ ),…(12分)
),…(12分)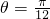 时,|BC|取得最大值
时,|BC|取得最大值 .…(13分)
.…(13分) )-cosθ|+|sin(θ+
)-cosθ|+|sin(θ+ )-sinθ|,…(8分)
)-sinθ|,…(8分) ,
, ≤θ+
≤θ+ ≤
≤ <π,即0≤θ<θ+
<π,即0≤θ<θ+ <π,
<π, =cosθ-cos(θ+
=cosθ-cos(θ+ ).…(9分)
).…(9分) ,
, -θ≥(θ+
-θ≥(θ+ )-
)- ,
,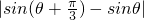 =sin(θ+
=sin(θ+ )-sinθ,…10分
)-sinθ,…10分 )+sin(θ+
)+sin(θ+ )-sinθ
)-sinθ )+cos(θ+
)+cos(θ+ )
) sin(θ+
sin(θ+ ),…(12分)
),…(12分) ,|BC|取得最大值
,|BC|取得最大值 .…(13分)
.…(13分) ),sin(θ+
),sin(θ+ ))可求得
))可求得 的坐标,利用两角和与差的三角函数公式即可求得
的坐标,利用两角和与差的三角函数公式即可求得 .
. +θ,
+θ, =
= ,利用三角函数的定义可求得D点的坐标为:D(cos(θ+
,利用三角函数的定义可求得D点的坐标为:D(cos(θ+ ),sin(θ+
),sin(θ+ )),即
)),即 的坐标;
的坐标; )|+|sin(θ+
)|+|sin(θ+ ))|,而θ∈[0,
))|,而θ∈[0, ],可求得θ+
],可求得θ+ ∈[
∈[ ,π],从而可得|BC|=-cos(θ+
,π],从而可得|BC|=-cos(θ+ )+sin(θ+
)+sin(θ+ ),整理可得|BC|=
),整理可得|BC|= sin(θ+
sin(θ+ ),继而可得答案;
),继而可得答案; )-cosθ|+|sin(θ+
)-cosθ|+|sin(θ+ )-sinθ|,由0≤θ≤
)-sinθ|,由0≤θ≤ ,可得0<θ+
,可得0<θ+ <π,从而
<π,从而 =cosθ-cos(θ+
=cosθ-cos(θ+ ),同理
),同理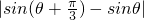 =sin(θ+
=sin(θ+ )-sinθ,于是|BC|=sin(θ+
)-sinθ,于是|BC|=sin(θ+ )+cos(θ+
)+cos(θ+ ),再利用辅助角公式即可得答案.
),再利用辅助角公式即可得答案.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案科目:高中数学 来源: 题型:
 (2012•泉州模拟)将边长为1的正三角形ABC按如图所示的方式放置,其中顶点A与坐标原点重合.记边AB所在直线的倾斜角为θ,已知θ∈[0,
(2012•泉州模拟)将边长为1的正三角形ABC按如图所示的方式放置,其中顶点A与坐标原点重合.记边AB所在直线的倾斜角为θ,已知θ∈[0,| π |
| 3 |
| BC |
查看答案和解析>>
科目:高中数学 来源:2010年高考试题分项版理科数学之专题十六算法初步 题型:填空题
将边长为1的正三角形薄片,沿一条平行于底边的直线剪成两块,其中一块是梯形,记S= ,则S的最小值是_______
_______
,则S的最小值是_______
_______
查看答案和解析>>
科目:高中数学 来源:2010年高考试题分项版理科数学之专题三数列 题型:填空题
将边长为1的正三角形薄片,沿一条平行于底边的直线剪成两块,其中一块是梯形,记S= ,则S的最小值是_______
_______
,则S的最小值是_______
_______
查看答案和解析>>
科目:高中数学 来源:2010年高考试题分项版理科数学之专题七直线与圆的方程 题型:填空题
将边长为1的正三角形薄片,沿一条平行于底边的直线剪成两块,其中一块是梯形,记S= ,则S的最小值是_______
_______
,则S的最小值是_______
_______
查看答案和解析>>
科目:高中数学 来源:2010年普通高等学校招生全国统一考试(江苏卷)数学试题 题型:填空题
将边长为1的正三角形薄片,沿一条平行于底边的直线剪成两块,其中一块是梯形,记S= ,则S的最小值是_______
_______
,则S的最小值是_______
_______
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com