
����Ŀ�����������������룬���ϵ����Ĵ�ѧԽ��Խ�ܵ���������������±������ϵ���ij��ѧ�������¼ȡƽ������ʡһ���߶Աȱ���
��� | 2014 | 2015 | 2016 | 2017 | 2018 |
��ݴ��� | 1 | 2 | 3 | 4 | 5 |
ʡһ���� | 505 | 500 | 525 | 500 | 530 |
¼ȡƽ����533 | 534 | 566 | 547 | 580 | |
¼ȡƽ������ʡһ���߷ֲ�y | 28 | 34 | 41 | 47 | 50 |
��1�������ϱ����ݿ�֪��y��t֮�����������ع�ϵ����y����t�����Իع鷽�̣�
��2�����������ݿ�֪���ô�ѧÿ���¼ȡ����X������̬�ֲ�![]() ������
������![]() Ϊ����ô�ѧ��¼ȡƽ����,����2019���ʡһ����Ϊ520�֣��2019��߿�����569�֣�����ϲ��������ѧ�����һ־Ը��������ø�����ͳ��֪ʶ�����һ�������Ľ���.����һ־Ը¼ȡ�����Ե���
Ϊ����ô�ѧ��¼ȡƽ����,����2019���ʡһ����Ϊ520�֣��2019��߿�����569�֣�����ϲ��������ѧ�����һ־Ը��������ø�����ͳ��֪ʶ�����һ�������Ľ���.����һ־Ը¼ȡ�����Ե���![]() ���������������
���������������
�ο���ʽ��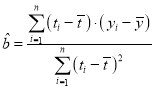 ��
��![]() .
.
�ο����ݣ�![]() ��
��![]() .
.
���𰸡���1��![]() ����2���������һ־Ը���������ô�ѧ.
����2���������һ־Ը���������ô�ѧ.
��������
��1���ɱ��е����ݴ��빫ʽ�������![]() ��
��![]() �����ɵõ�
�����ɵõ�![]() ����
����![]() �����Իع鷽�̣�
�����Իع鷽�̣�
��2����ϣ�1�������2019��¼ȡƽ���֣��ٸ��ݸô�ѧÿ���¼ȡ����X������̬�ֲ�![]() ������̬�ֲ������ʿɼ�������¼ȡ�ĸ��ʣ��ɴ˵õ����ۡ�
������̬�ֲ������ʿɼ�������¼ȡ�ĸ��ʣ��ɴ˵õ����ۡ�
��1������֪��![]() ��
��
![]()
���Եã�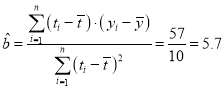
![]()
������ع鷽��Ϊ��![]() ��
��
��2���ɣ�1��֪����![]() ʱ��
ʱ��![]() ���ʸô�ѧ2019���¼ȡƽ����Ϊ577.1��.
���ʸô�ѧ2019���¼ȡƽ����Ϊ577.1��.
����Ϊ![]()
�������¼ȡ�ĸ��ʣ�
![]()
�ʽ������һ־Ը���������ô�ѧ.


 ÿ��10���ӿ�����������������ϵ�д�
ÿ��10���ӿ�����������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������ṩ��ij�����������·֣�30�죩����������µ�ͳ�Ʊ����£�
���������t����� |
|
|
|
|
���� | 6 | 12 |
|
|
���ڹ��������ͳ�Ʊ���īˮ��Ⱦ��![]() ��
��![]() ���ݲ���������������ṩ��������ʾ�����·ݵ���������²�����
���ݲ���������������ṩ��������ʾ�����·ݵ���������²�����![]() ��Ƶ��Ϊ0.9.
��Ƶ��Ϊ0.9.
��1������Ƶ�ʿ������ʣ���![]() ��
��![]() ��ֵ��
��ֵ��
��2������������¸߸�![]() ��Ϊ�������ġ�������������������֪�����������2��2�����������ݴ��Ʋ��Ƿ���95%�İ�����Ϊ�����������������������ϡ��������йأ�˵������.
��Ϊ�������ġ�������������������֪�����������2��2�����������ݴ��Ʋ��Ƿ���95%�İ�����Ϊ�����������������������ϡ��������йأ�˵������.
�������� | �Ǹ������� | �ϼ� | |
���� | 1 | ||
������ | 6 | ||
�ϼ� |
��![]()
P(K2��R) | 0.10 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
K | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ABC�Ķ�������ֱ���A��7����3����B��2����8����C��5��1����
��1����AB��ֱƽ���ߵķ��̣���Ϊһ��ʽ����
��2������ABC���Բ�ķ��̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����12�֣�������{an}�ǹ���Ϊ�����ĵȱ����У�a1=2��a3��a2=12��
��1��������{an}��ͨ�ʽ��
��2��������{bn}������Ϊ1������Ϊ2�ĵȲ����У�������{an+bn}��ǰn���Sn��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����ÿ������һ�ֲ�Ʒ![]() �֣�ÿ�������IJ�Ʒ����������ϣ������۶�Ϊ
�֣�ÿ�������IJ�Ʒ����������ϣ������۶�Ϊ![]() ��Ԫ����Ʒ�۸����Ų����仯�������仯��������ʱ��IJ����� �õ���
��Ԫ����Ʒ�۸����Ų����仯�������仯��������ʱ��IJ����� �õ���![]() ��һ��ͳ���������±�:
��һ��ͳ���������±�:
�ղ��� | 1 | 2 | 3 | 4 | 5 |
�������� | 5 | 12 | 16 | 19 | 21 |
��1�����ж�![]() ��
��![]() �У��ĸ�ģ���ʺϵ���
�У��ĸ�ģ���ʺϵ���![]() ֮��Ĺ�ϵ���ɴӺ����������Ʒ�����������ɣ�
֮��Ĺ�ϵ���ɴӺ����������Ʒ�����������ɣ�
��2����������жϼ���������ݺ�ʽ�����![]() ����
����![]() �Ļع鷽�̣������Ƶ��ղ���
�Ļع鷽�̣������Ƶ��ղ���![]() ʱ�������۶��Ƕ���?
ʱ�������۶��Ƕ���?
�ο����ݣ�![]() ��
��![]()
![]()
���Իع鷽��![]() �У�
�� ��
��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���![]() �У�
�У�![]() ΪCD���е㣬��
ΪCD���е㣬��![]() ��AE����
��AE����![]() ��λ�ã�ʹ��ƽ��
��λ�ã�ʹ��ƽ��![]() ƽ��
ƽ��![]() ��
��

��1��֤����ƽ��![]() ƽ��
ƽ��![]() ��
��
��2����ƽ��![]() ��ƽ��
��ƽ��![]() ���ɶ���ǵ�����ֵ.
���ɶ���ǵ�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x����loga��x+a����a��0��a��1����ͼ����㣨��1��0����g��x����f��x��+f����x����
��������g��x���Ķ�����
����д������g��x���ĵ������䣬����g��x�������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��Ϊ��Լ��ˮ���ƻ��ڱ������о���������ˮ���������Ϊ�˽�Ϊ������ȷ�������ճ���ˮ���ı���ͨ�����������100λ����ij����¾���ˮ������λ���֣����ұ���100λ�����¾���ˮ����Ƶ�ʷֲ����������ұ�����������⣺
���� | Ƶ�� | Ƶ�� |
[0,1) | 10 | 0.10 |
[1,2) |
| 0.20 |
[2,3) | 30 | 0.30 |
[3,4) | 20 |
|
[4,5) | 10 | 0.10 |
[5,6] | 10 | 0.10 |
�ϼ� | 100 | 1.00 |

��1�����ұ���![]() ��
��![]() ��ֵ��
��ֵ��
��2���뽫Ƶ�ʷֲ�ֱ��ͼ����������������ֱ��ͼ���Ƹ���ÿλ�����¾���ˮ��������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��![]() ������
������![]() ��.
��.
��1����![]() ʱ���ⲻ��ʽ
ʱ���ⲻ��ʽ![]() ��
��
��2����![]() ʱ���жϲ��ö��巨֤��������
ʱ���жϲ��ö��巨֤��������![]() �ĵ����ԣ�
�ĵ����ԣ�
��3�����ۺ���![]() ����ż�ԣ���˵������.
����ż�ԣ���˵������.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com