
【题目】下列选项中,说法正确的是( )
A.“![]() ”的否定是“
”的否定是“![]() ”
”
B.若向量![]() 满足
满足![]() ,则
,则![]() 与
与![]() 的夹角为钝角
的夹角为钝角
C.若![]() ,则
,则![]()
D.“![]() ”是“
”是“![]() ”的必要条件
”的必要条件
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知下列命题:
①在线性回归模型中,相关指数![]() 越接近于1,表示回归效果越好;
越接近于1,表示回归效果越好;
②两个变量相关性越强,则相关系数r就越接近于1;
③在回归直线方程![]() 中,当解释变量
中,当解释变量![]() 每增加一个单位时,预报变量
每增加一个单位时,预报变量![]() 平均减少0.5个单位;
平均减少0.5个单位;
④两个模型中残差平方和越小的模型拟合的效果越好.
⑤回归直线![]() 恒过样本点的中心
恒过样本点的中心![]() ,且至少过一个样本点;
,且至少过一个样本点;
⑥若![]() 的观测值满足
的观测值满足![]() ≥6.635,我们有99%的把握认为吸烟与患肺病有关系,那么在100个吸烟的人中必有99人患有肺病;
≥6.635,我们有99%的把握认为吸烟与患肺病有关系,那么在100个吸烟的人中必有99人患有肺病;
⑦从统计量中得知有95%的把握认为吸烟与患肺病有关系,是指有5%的可能性使得推断出现错误. 其中正确命题的序号是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某旅游爱好者计划从3个亚洲国家A1,A2,A3和3个欧洲国家B1,B2,B3中选择2个国家去旅游.
(1)若从这6个国家中任选2个,求这2个国家都是亚洲国家的概率;
(2)若从亚洲国家和欧洲国家中各选1个,求这两个国家包括A1,但不包括B1的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某景区内有两条道路![]() 、
、![]() ,现计划在
,现计划在![]() 上选择一点
上选择一点![]() ,新建道路
,新建道路![]() ,并把
,并把![]() 所在的区域改造成绿化区域.已知
所在的区域改造成绿化区域.已知![]() ,
,![]() ,
,![]() .若绿化区域
.若绿化区域![]() 改造成本为
改造成本为![]() 万元
万元![]() ,新建道路
,新建道路![]() 成本为
成本为![]() 万元
万元![]() .
.
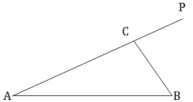
(1)①设![]() ,写出该计划所需总费用
,写出该计划所需总费用![]() 的表达式,并写出
的表达式,并写出![]() 的范围;
的范围;
②设![]() ,写出该计划所需总费用
,写出该计划所需总费用![]() 的表达式,并写出
的表达式,并写出![]() 的范围;
的范围;
(2)从上面两个函数关系中任选一个,求点![]() 在何处时改造计划的总费用最小.
在何处时改造计划的总费用最小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学为研究“网络游戏对当代青少年的影响”作了一次调查,共调查了50名同学,其中男生26人,有8人不喜欢玩游戏,而调查的女生中有9人喜欢玩游戏.
(1)根据以上数据完成2×2的列联表;
(2)根据以上数据,在犯错误的概率不超过0.025的前提下,能否认为“喜欢玩电脑游戏与性别有关系”?
男生 | 女生 | 总计 | |
喜欢玩游戏 | |||
不喜欢玩游戏 | |||
总计 |

| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
k | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某机构为了解某地区中学生在校月消费情况,随机抽取了 100名中学生进行调查.如图是根据调査的结果绘制的学生在校月消费金额的频率分布直方图.已知![]() 三个金额段的学生人数成等差数列,将月消费金额不低于550元的学生称为“高消费群”.
三个金额段的学生人数成等差数列,将月消费金额不低于550元的学生称为“高消费群”.
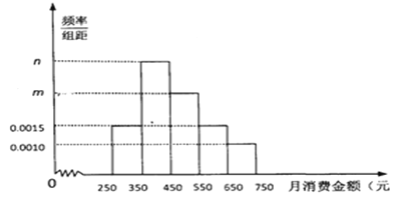
(1)求![]() 的值,并求这100名学生月消费金额的样本平均数
的值,并求这100名学生月消费金额的样本平均数![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
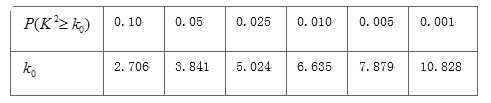
(2)根据已知条件完成下面![]() 列联表,并判断能否有
列联表,并判断能否有![]() 的把握认为“高消费群”与性别有关?
的把握认为“高消费群”与性别有关?

附: ![]() (其中
(其中![]() 样本容量)
样本容量)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com