
【题目】已知函数![]() 的定义域为
的定义域为![]() ,设
,设![]() ,
,![]() .
.
(Ⅰ)试确定t的取值范围,使得函数![]() 在
在![]() 上为单调函数;
上为单调函数;
(Ⅱ)求证:![]() ;
;
(Ⅲ)求证:对于任意的![]() ,总存在
,总存在![]() ,满足
,满足![]() ,又若方程
,又若方程![]() 在
在![]() 上有唯一解,请确定t的取值范围.
上有唯一解,请确定t的取值范围.
【答案】(Ⅰ)![]() ;(Ⅱ)见解析;(Ⅲ)见解析
;(Ⅱ)见解析;(Ⅲ)见解析
【解析】
(Ⅰ)求导得![]() ,从而可得
,从而可得![]() 在
在![]() ,
,![]() 上递增,在
上递增,在![]() 上递减,从而确定
上递减,从而确定![]() 的取值范围;
的取值范围;
(Ⅱ)借助(Ⅰ)可知,![]() 在
在![]() 处取得极小值
处取得极小值![]() ,求出
,求出![]() ,则
,则![]() 在
在![]() ,
,![]() 上的最小值为
上的最小值为![]() ,从而得证;
,从而得证;
(Ⅲ)化简![]() ,从而将
,从而将![]() 化为
化为![]() ,令
,令![]() ,则证明方程
,则证明方程![]() 在
在![]() 上有解,并讨论解的个数;由二次函数的性质讨论即可.
上有解,并讨论解的个数;由二次函数的性质讨论即可.
(Ⅰ)因为![]() ,
,
令![]() ,得:
,得:![]() 或
或![]() ;令
;令![]() ,得:
,得:![]()
所以![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
要使![]() 在
在![]() 为单调函数,则
为单调函数,则![]()
所以![]() 的取值范围为
的取值范围为![]()
(Ⅱ)证:因为![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,所以
上单调递减,所以![]() 在
在![]() 处取得极小值
处取得极小值![]() .
.
又![]() ,所以
,所以![]() 在
在![]() 的最小值为
的最小值为![]() ,
,
从而当![]() 时,
时,![]() ,即
,即![]() .
.
(Ⅲ)证:因为![]() ,所以
,所以![]() ,即为
,即为![]()
令![]() ,从而问题转化为证明方程
,从而问题转化为证明方程![]() 在
在![]() 上有解,
上有解,
并讨论解的个数,因为![]() ,
,
![]()
当![]() 或
或![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 上有解,且只有一解.
上有解,且只有一解.
②当![]() 时,
时,![]() 且
且![]() ,但由于
,但由于![]() ,所以
,所以![]() 在
在![]() 上有解,且有两解
上有解,且有两解
③当![]() 时,由
时,由![]() 得:
得:![]() 或
或![]() ,
,![]() 在
在![]() 上有且只有一解;
上有且只有一解;
当![]() 时,由
时,由![]() 得:
得:![]() 或
或![]() ,所以
,所以![]() 在
在![]() 上也只有一解
上也只有一解
综上所述,对任意的![]() ,总存在
,总存在![]()
当方程![]() 在
在![]() 上有唯一解,
上有唯一解,![]() 的取值范围为
的取值范围为![]()


科目:高中数学 来源: 题型:
【题目】教材曾有介绍:圆![]() 上的点
上的点![]() 处的切线方程为
处的切线方程为![]() 。我们将其结论推广:椭圆
。我们将其结论推广:椭圆![]() 上的点
上的点![]() 处的切线方程为
处的切线方程为![]() ,在解本题时可以直接应用。已知,直线
,在解本题时可以直接应用。已知,直线![]() 与椭圆
与椭圆![]() 有且只有一个公共点.
有且只有一个公共点.
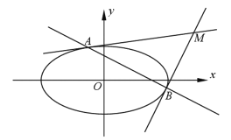
(1)求![]() 的值;
的值;
(2)设![]() 为坐标原点,过椭圆
为坐标原点,过椭圆![]() 上的两点
上的两点![]() 、
、![]() 分别作该椭圆的两条切线
分别作该椭圆的两条切线![]() 、
、![]() ,且
,且![]() 与
与![]() 交于点
交于点![]() 。当
。当![]() 变化时,求
变化时,求![]() 面积的最大值;
面积的最大值;
(3)在(2)的条件下,经过点![]() 作直线
作直线![]() 与该椭圆
与该椭圆![]() 交于
交于![]() 、
、![]() 两点,在线段
两点,在线段![]() 上存在点
上存在点![]() ,使
,使![]() 成立,试问:点
成立,试问:点![]() 是否在直线
是否在直线![]() 上,请说明理由.
上,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点与短轴两端点构成一个面积为2的等腰直角三角形,
的右焦点与短轴两端点构成一个面积为2的等腰直角三角形,![]() 为坐标原点.
为坐标原点.
(1)求椭圆![]() 的方程;
的方程;
(2)设点![]() 在椭圆
在椭圆![]() 上,点
上,点![]() 在直线
在直线![]() 上,且
上,且![]() ,求证:
,求证:![]() 为定值;
为定值;
(3)设点![]() 在椭圆
在椭圆![]() 上运动,
上运动,![]() ,且点
,且点![]() 到直线
到直线![]() 的距离为常数
的距离为常数![]() ,求动点
,求动点![]() 的轨迹方程.
的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设甲乙两地相距100海里,船从甲地匀速驶到乙地,已知某船的最大船速是36海里/时:当船速不大于每小时30海里/时,船每小时使用的燃料费用和船速成正比;当船速不小于每小时30海里/时,船每小时使用的燃料费用和船速的平方成正比;当船速为30海里/时,它每小时使用的燃料费用为300元;其余费用(不论船速为多少)都是每小时480元;
(1)试把每小时使用的燃料费用P(元)表示成船速v(海里/时)的函数;
(2)试把船从甲地行驶到乙地所需要的总费用Y表示成船速v的函数;
(3)当船速为每小时多少海里时,船从甲地到乙地所需要的总费用最少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某农场规划将果树种在正方形的场地内.为了保护果树不被风吹,决定在果树的周围种松树. 在下图里,你可以看到规划种植果树的列数(n),果树数量及松树数量的规律:

(1)按此规律,n = 5时果树数量及松树数量分别为多少;并写出果树数量![]() ,及松树数量
,及松树数量![]() 关于n的表达式
关于n的表达式
(2)定义:![]()
![]() 为
为![]() 增加的速度;现农场想扩大种植面积,问:哪种树增加的速度会更快?并说明理由
增加的速度;现农场想扩大种植面积,问:哪种树增加的速度会更快?并说明理由
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,动点
中,动点![]() 到定点
到定点![]() 的距离与它到直线
的距离与它到直线![]() 的距离相等.
的距离相等.
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)设动直线![]() 与曲线
与曲线![]() 相切于点
相切于点![]() ,与直线
,与直线![]() 相交于点
相交于点![]() .
.
证明:以![]() 为直径的圆恒过
为直径的圆恒过![]() 轴上某定点.
轴上某定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:对于数列![]() ,如果存在常数
,如果存在常数![]() ,使对任意正整数
,使对任意正整数![]() ,总有
,总有![]() 成立,那么我们称数列
成立,那么我们称数列![]() 为“
为“![]() ﹣摆动数列”.
﹣摆动数列”.
(1)设![]() ,
,![]() ,
,![]() ,判断数列
,判断数列![]() 、
、![]() 是否为“
是否为“![]() ﹣摆动数列”,并说明理由;
﹣摆动数列”,并说明理由;
(2)已知“![]() ﹣摆动数列”
﹣摆动数列”![]() 满足:
满足:![]() ,
,![]() .求常数
.求常数![]() 的值;
的值;
(3)设![]() ,
,![]() ,且数列
,且数列![]() 的前
的前![]() 项和为
项和为![]() .求证:数列
.求证:数列![]() 是“
是“![]() ﹣摆动数列”,并求出常数
﹣摆动数列”,并求出常数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知点F(1,0)为抛物线y2=2px(p>0)的焦点,过点F的直线交抛物线于A、B两点,点C在抛物线上,使得△ABC的重心G在x轴上.
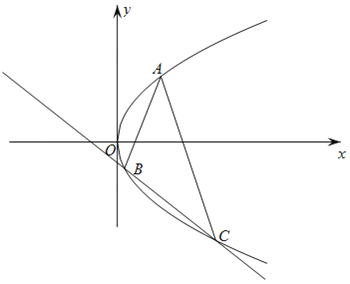
(1)求p的值及抛物线的准线方程 ;
(2)求证:直线OA与直线BC的倾斜角互补;
(3)当xA∈(1,2)时,求△ABC面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com