B
分析:根据实数相反数的定义,得到①是真命题;用举反例的方法可得②是假命题;利用一元二次方程根的判别式,可得③是真命题;根据原命题与逆否命题同真同假,结合原命题是一个假命题,得到④不正确.由此得到正确选项.
解答:对于①,“若x+y=0,则x、y互为相反数”的逆命题是“若x、y互为相反数,则x+y=0”,
根据相反数的定义,可得逆命题是个真命题,故①正确;
对于②,“全等三角形的面积相等”的否命题是“不全等的两个三角形面积不相等”,这是假命题,
反例:△ABC是底边长为2,高为1的等腰三角形,△A'B'C'是两直角边分别是1、2的直角三角形,
显然△ABC与△A'B'C'不全等,但是它们的面积都等于1,故②错误;
对于③,“若q≤1,则x2+2x+q=0有实根”的逆命题是“若x2+2x+q=0有实根,则q≤1”,
∵方程x2+2x+q=0的根的判别式△=4-4q,
∴方程有实数根时,4-4q≥0,可得q≤1,故③正确;
对于④,当c=0时,命题“若a>b,则ac2>bc2”不正确,所以“若a>b,则ac2>bc2”是假命题
而一个命题的逆否命题与原命题的真值相同,所以逆否命题也是一个假命题,故④不正确.
综上所述,真命题是①③
故选B
点评:本题以命题的真假判断为载体,考查了相反数的定义、三角形全等的性质和一元二次方程根的判别式等知识点,属于基础题.



 教材全解字词句篇系列答案
教材全解字词句篇系列答案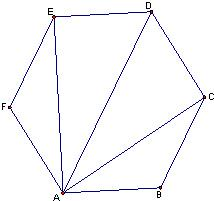 如图,正六边形ABCDEF中,有下列四个命题:其中真命题的代号是
如图,正六边形ABCDEF中,有下列四个命题:其中真命题的代号是