Question

抛物线y²=8x上的点P到两直线l₁：x=-2，l₂：12x-5y+15=0的距离之和的最小值为

3

．

Answer 1

分析：由抛物线方程求出其焦点坐标和准线方程，把抛物线y²=8x上的点P到两直线l₁：x=-2，l₂：12x-5y+15=0的距离之和的最小值转化为焦点到l₂：12x-5y+15=0的距离，由点到直线的距离公式求解．

解答：解：如图，

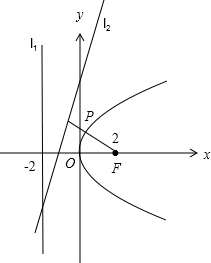
由抛物线y²=8x，得其焦点F（2，0），准线方程为x=-2．
∴l₁：x=-2为抛物线的准线，
P到两直线l₁：x=-2，l₂：12x-5y+15=0的距离之和即为P到F和l₂：12x-5y+15=0的距离之和．
最小值为F到l₂：12x-5y+15=0的距离，等于

|12×2-5×0+15|

122+(-5)2

=

39

13

=3．
故答案为3．

点评：本题考查了直线与圆锥曲线的关系，考查了数形结合的解题思想方法和数学转化思想方法，是中档题．