设函数f(x)=x+ax2+blnx,曲线y=f(x)过点P(1,0),且在点P处的切线斜率为2.
(Ⅰ)求a,b的值;
(Ⅱ)求f(x)的极值点;
(Ⅲ)对定义域内任意一个x,不等式f(x)≤2x-2是否恒成立,若成立,请证明;若不成立,请说明理由.
解:(Ⅰ)∵f(x)=x+ax
2+blnx(x>0)
∴
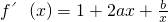
,
∵y=f(x)在点P(1,0)处的切线斜率为2,
∴
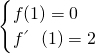
即
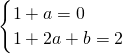
解得

,
∴a=-1,b=3.
(Ⅱ)∵f(x)=x-x
2+3lnx(x>0)

得
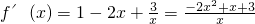
,
即
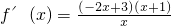
由x>0可得,
当f'(x)>0时,解得
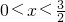
,
当f'(x)<0时,解得

.
列表可得:
故f(x)只有极大值点,且极大值点为

.
(Ⅲ)令g(x)=f(x)-2x+2,得g(x)=-x
2-x+2+3lnx(x>0),

∴
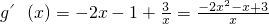
,
即
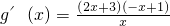
.
由x>0可得,
当g'(x)>0时,解得0<x<1;
当g'(x)<0时,x>1.
列表可得:
由表可知g(x)的最大值为g(1)=0.
即g(x)≤0恒成立,因此f(x)≤2x-2恒成立.
分析:(Ⅰ)利用导数的几何意义及切点即可得出a、b的值;
(Ⅱ)利用f
′(x)=0及x>0解出x的值,进而利用极值的定义进行判定即可求出;
(Ⅲ)对定义域内任意一个x,不等式f(x)≤2x-2是否恒成立?g(x)=f(x)-2x+2≤0在(0,+∞)上恒成立?g(x)
max≤0,x∈(0,+∞).利用导数求出函数g(x)的极大值,进而求出其最大值即可判断出答案.
点评:熟练掌握导数的几何意义和利用导数研究函数的极值、最值的方法是解题的关键.注意分类讨论的思想方法和转化思想的应用.

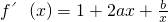 ,
,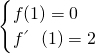 即
即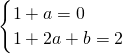
 ,
,
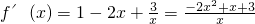 ,
,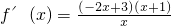
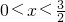 ,
, .
. .
.
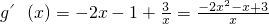 ,
,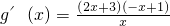 .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案