
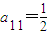 ,a24=1,
,a24=1,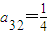 .
.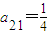 ,求a12和a13的值.
,求a12和a13的值.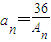 ,联mbn+1=2(an+mbn)(m为非零常数),
,联mbn+1=2(an+mbn)(m为非零常数),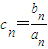 ,且c12+c72=100,求c1+c2+…c7的取值范围.
,且c12+c72=100,求c1+c2+…c7的取值范围. ,设Bn=d1•d2…dn(n∈N),求数列{Bn}中最大项的项数.
,设Bn=d1•d2…dn(n∈N),求数列{Bn}中最大项的项数. ,
, ,由a11,a12,a13,a14成等差可求
,由a11,a12,a13,a14成等差可求 解出d,q,从而可求an1,An,进而可求an
解出d,q,从而可求an1,An,进而可求an 即
即 ,利用等差数列的求和公式及基本不等式可求
,利用等差数列的求和公式及基本不等式可求 是一个正项递减数列可得dn≥1时Bn>Bn-1,dn<1时Bn<Bn-1,若{Bn}中最大项满足
是一个正项递减数列可得dn≥1时Bn>Bn-1,dn<1时Bn<Bn-1,若{Bn}中最大项满足 可求
可求 ,∴
,∴


 ,
, ′
′

 ∴an=2n(1≤n≤8,n∈N)
∴an=2n(1≤n≤8,n∈N)
 ∴
∴ ∴{cn}是等差数列
∴{cn}是等差数列


 是一个正项递减数列
是一个正项递减数列 ⇒
⇒


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2008-2009学年度北京五中第一学期高三数学期中考试 题型:044
设数列{an}的前n项和为Sn,对一切n∈N*,点![]() 都在函数
都在函数![]() 的图象上.
的图象上.
(1)求a1,a2,a3的值,并求通项an;
(2)将数列{an}依次按1项、2项、3项、4项循环地分为(a1),(a2,a3),(a4,a5,a6),(a7,a8,a9,a10);(a11),(a12,a13),(a14,a15,a16),(a17,a18,a19,a20);(a21),…,分别计算各个括号内各数之和,设由这些和按原来括号的前后顺序构成的数列为{bn},求b5+b100的值;
(3)设An为数列 的前n项积,是否存在实数a,使得不等式
的前n项积,是否存在实数a,使得不等式![]() 对一切n∈N*都成立?若存在,求出a的取值范围;若不存在,请说明理由.
对一切n∈N*都成立?若存在,求出a的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
A.120 B.105 C.90 D.75
查看答案和解析>>
科目:高中数学 来源:专项题 题型:单选题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com