
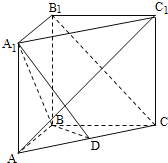
【题目】如图所示,在直三棱柱![]() 中,
中,![]() ,
,![]() 平面
平面![]() ,D为AC的中点
,D为AC的中点![]()
![]() Ⅰ
Ⅰ![]() 求证:
求证:![]() 平面
平面![]() ;
;
![]() Ⅱ
Ⅱ![]() 求证:
求证:![]() 平面
平面![]() .
.
【答案】(Ⅰ)![]() ∥平面
∥平面![]() ,证明略。
,证明略。
(Ⅱ)![]() ,证明略。
,证明略。
【解析】
(Ⅰ)证明:如图连结![]() ,
,
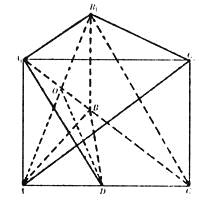
![]() ………………………………………………………………1分
………………………………………………………………1分
则O为![]() 中点,……………………………………………………………………………2分
中点,……………………………………………………………………………2分
连OD,∵D为AC中点,
在△![]() 中,有OD∥
中,有OD∥![]() .………………………………………………………………3分
.………………………………………………………………3分
又![]() 平面
平面![]() ,……………………………………4分
,……………………………………4分
![]()
![]() 平面
平面![]() ,……………………………………5分
,……………………………………5分
∴![]() ∥平面
∥平面![]() .……………………………………6分
.……………………………………6分
(Ⅱ)证明:由![]() ,
,
三棱柱![]() 为直三棱柱,
为直三棱柱,
![]() 为正方形,
为正方形,
![]() …………………………………………7分
…………………………………………7分
又![]() ,
,
![]() ,
,
![]() ,………………………………………8分
,………………………………………8分
又![]() ,
,
![]()
![]()
![]()
又![]()
![]() .……………………………………………………………………9分
.……………………………………………………………………9分
又![]()
![]()
![]() ……………………………………………………………………10分
……………………………………………………………………10分
又![]()
![]()
![]() ………………………………………………………………11分
………………………………………………………………11分
![]() ……………………………………………………………12分
……………………………………………………………12分


科目:高中数学 来源: 题型:
【题目】2019年篮球世界杯在中国举行,中国男篮由于主场作战而备受观众瞩目.为了调查国人对中国男篮能否进入十六强持有的态度,调查人员随机抽取了男性观众与女性观众各100名进行调查,所得情况如下表所示:
男性观众 | 女性观众 | |
认为中国男篮能够进入十六强 | 60 | |
认为中国男篮不能进入十六强 |
若在被抽查的200名观众中随机抽取1人,抽到认为中国男篮不能进入十六强的女性观众的概率为![]() .
.
(1)完善上述表格;
(2)是否有99%的把握认为性别与对中国男篮能否进入十六强持有的态度有关?
附: ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司的新能源产品上市后在国内外同时销售,已知第一批产品上市销售40天内全部售完,该公司对这批产品上市后的国内外市场销售情况进行了跟踪调查,如图所示,其中图①中的折线表示的是国外市场的日销售量与上市时间的关系;图②中的抛物线表示的是国内市场的日销售量与上市时间的关系;下表表示的是产品广告费用、产品成本、产品销售价格与上市时间的关系.
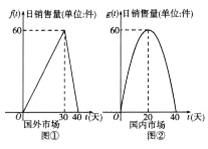

(1)分别写出国外市场的日销售量![]() 、国内市场的日销售量
、国内市场的日销售量![]() 与产品上市时间
与产品上市时间![]() 的函数关系式;
的函数关系式;
(2)产品上市后的哪几天,这家公司的日销售利润超过260万元?
(日销售利润=(单件产品销售价-单件产品成本)×日销售量-当天广告费用,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】科学家发现某种特别物质的温度![]() (单位:摄氏度)随时间
(单位:摄氏度)随时间![]() (时间:分钟)的变化规律满足关系式:
(时间:分钟)的变化规律满足关系式:![]() (
(![]() ,
,![]() ).
).
(1)若![]() ,求经过多少分钟,该物质的温度为5摄氏度;
,求经过多少分钟,该物质的温度为5摄氏度;
(2)如果该物质温度总不低于2摄氏度,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 在双曲线
在双曲线![]()
![]() (
(![]() ,
,![]() )上,且双曲线的一条渐近线的方程是
)上,且双曲线的一条渐近线的方程是![]() .
.
(1)求双曲线![]() 的方程;
的方程;
(2)若过点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 与双曲线
与双曲线![]() 有两个不同的交点,求实数
有两个不同的交点,求实数![]() 的取值范围;
的取值范围;
(3)设(2)中直线![]() 与双曲线
与双曲线![]() 交于
交于![]() 两个不同的点,若以线段
两个不同的点,若以线段![]() 为直径的圆经过坐标原点,求实数
为直径的圆经过坐标原点,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
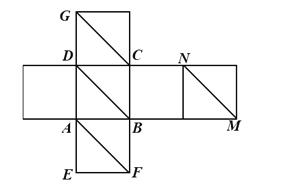
【题目】如图所示为一正方体的平面展开图,在这个正方体中,有下列四个命题:
①AF⊥GC;
②BD与GC成异面直线且夹角为60;
③BD∥MN;
④BG与平面ABCD所成的角为45.
其中正确的个数是( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com