|
|
|
设双曲线C的两个焦点为 ， ，一个顶点式(1，0)，则C的方程为
________．
|
|
|
练习册系列答案
相关习题
科目：高中数学
来源：课标综合版 专题复习
题型：
|
|
|
已知某地区中小学学生人数和近视情况分别如图1和如图2所示，为了解该地区中下学生的近视形成原因，用分层抽样的方法抽取2％的学生进行调查，则样本容量和抽取的高中生近视人数分别为
|
| [ ] |
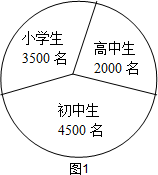
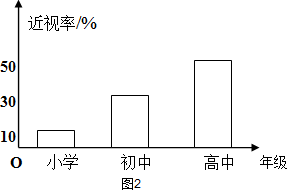
A． |
100，10
|
B． |
200，10
|
C． |
100，20
|
D． |
200，20
|
|
|
查看答案和解析>>
科目：高中数学
来源：课标综合版 专题复习
题型：
|
|
|
若函数y＝logax(a＞0，且a≠1)的图像如图所示，则下列函数图像正确的是
|
| [ ] |
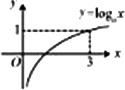
A． |
|
B． |
|
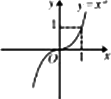
C． |
|
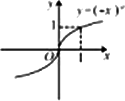
D． |
|
|
|
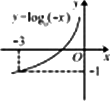
查看答案和解析>>
科目：高中数学
来源：课标综合版 专题复习
题型：
|
|
|
已知矩阵A的逆矩阵 ．
(Ⅰ)求矩阵A；
(Ⅱ)求矩阵A－1的特征值以及属于每个特征值的一个特征向量．
|
|
|
查看答案和解析>>
科目：高中数学
来源：课标综合版 专题复习
题型：
|
|
|
设a、b是实数，则“a＞b”是“a2＞b2”的
|
| [ ] |
A． |
充分而不必要条件
|
B． |
必要而不必要条件
|
C． |
充分必要条件
|
D． |
既不充分不必要条件
|
|
|
查看答案和解析>>
科目：高中数学
来源：课标综合版 专题复习
题型：
|
|
|
已知{an}是等差数列，满足a1＝3，a4＝12，数列{bn}满足b1＝4，b4＝20，且{bn－an}是等比数列．
(1)求数列{an}和{bn}的通项公式；
(2)求数列{bn}的前n项和．
|
|
|
查看答案和解析>>
科目：高中数学
来源：课标综合版 专题复习
题型：
|
|
|
下列函数中，在区间(0，＋∞)上为增函数的是
|
| [ ] |
A． |
y＝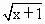
|
B． |
y＝(x－1)2
|
C． |
y＝2－x
|
D． |
y＝log0.5(x＋1)
|
|
|
查看答案和解析>>
科目：高中数学
来源：课标综合版 专题复习
题型：
|
|
|
已知椭圆C：x2＋2y2＝4，
(1)求椭圆C的离心率．
(2)设O为原点，若点A在椭圆C上，点B在直线y＝2上，且OA⊥OB，求直线AB与圆x2＋y2＝2的位置关系，并证明你的结论．
|
|
|
查看答案和解析>>
科目：高中数学
来源：课标综合版 专题复习
题型：
|
|
|
在三棱锥P－ABC中，△PAC和△PBC是边长为 的等边三角形，AB＝2，O是AB中点．
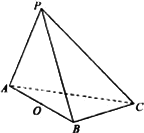
(Ⅰ)在棱PA上求一点M，使得OM∥平面PBC；
(Ⅱ)求证：平面PAB⊥平面ABC；
(Ⅲ)求二面角P－BC－A的余弦值．
|
|
|
查看答案和解析>>
