
【题目】已知![]() 的顶点
的顶点![]() ,
, ![]() 在椭圆
在椭圆![]() 上,
上, ![]() 在直线
在直线![]() 上,且
上,且![]() .
.
(![]() )求椭圆
)求椭圆![]() 的离心率.
的离心率.
(![]() )当
)当![]() 边通过坐标原点
边通过坐标原点![]() 时,求
时,求![]() 的长及
的长及![]() 的面积.
的面积.
(![]() )当
)当![]() ,且斜边
,且斜边![]() 的长最大时,求
的长最大时,求![]() 所在直线的方程.
所在直线的方程.
【答案】(1)![]() ;(2)
;(2)![]() ,面积为2;(3)
,面积为2;(3)![]() .
.
【解析】试题分析:(1)由椭圆方程得![]() ,
, ![]() ,
, ![]() ,由
,由![]() 即可得解;
即可得解;
(2)![]() 所直线的方程为
所直线的方程为![]() 与椭圆联立得
与椭圆联立得![]() ,
, ![]() ,原点到直线
,原点到直线![]() 的距离
的距离![]() ,从而得面积;
,从而得面积;
(3)设![]() 所在直线的方程为
所在直线的方程为![]() ,与椭圆联立得
,与椭圆联立得![]() ,设
,设![]() ,
, ![]() 两点坐标分别为
两点坐标分别为![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 利用韦达定理代入求最值即可.
利用韦达定理代入求最值即可.
试题解析:
(![]() )将椭圆
)将椭圆![]() 化为标准方程为
化为标准方程为 ,
,
∴![]() ,
, ![]() ,
, ![]() ,
,
∴椭圆![]() 的离心率
的离心率![]() .
.
(![]() )∵
)∵![]() ,且
,且![]() 边通过点
边通过点![]() ,∴
,∴![]() 所直线的方程为
所直线的方程为![]() .
.
设![]() ,
, ![]() 两点坐标分别为
两点坐标分别为![]() ,
, ![]() .
.
由![]() ,得
,得![]() .
.
∴![]() .
.
又∵![]() 边长的高
边长的高![]() 等于原点到直线
等于原点到直线![]() 的距离,∴
的距离,∴![]() ,
,
∴![]() 的面积
的面积![]() .
.
(![]() )设
)设![]() 所在直线的方程为
所在直线的方程为![]() ,
,
由![]() ,得
,得![]() .
.
∵![]() ,
, ![]() 在椭圆上,∴
在椭圆上,∴![]() .
.
设![]() ,
, ![]() 两点坐标分别为
两点坐标分别为![]() ,
, ![]() ,则
,则![]() ,
, ![]() ,
,
∴![]() .
.
又∵![]() 的长等于点
的长等于点![]() 到直线
到直线![]() 的距离,即
的距离,即![]() ,
,
∴![]() ,
,
∴当![]() 时,
时, ![]() 边最大,且满足
边最大,且满足![]() ,
,
此时![]() 所在直线的方程为
所在直线的方程为![]() .
.


科目:高中数学 来源: 题型:
【题目】学校某研究性学习小组在对学生上课注意力集中情况的调查研究中,发现其在40分钟的一节课中,注意力指数y与听课时间x(单位:分钟)之间的关系满足如图所示的图象,当x∈(0,12]时,图象是二次函数图象的一部分,其中顶点A(10,80),过点B(12,78);当x∈[12,40]时,图象是线段BC,其中C(40,50).根据专家研究,当注意力指数大于62时,学习效果最佳.
(1)试求y=f(x)的函数关系式;
(2)教师在什么时段内安排内核心内容,能使得学生学习效果最佳?请说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且过点
,且过点![]() .
.

(Ⅰ)求椭圆的标准方程;
(Ⅱ)四边形![]() 的顶点在椭圆上,且对角线
的顶点在椭圆上,且对角线![]() 、
、![]() 过原点
过原点![]() ,若
,若![]() ,
,
(1)求![]() 的最值;
的最值;
(2)求证;四边形![]() 的面积为定值.
的面积为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平行六面体ABCD-A1B1C1D1中,AA1⊥平面ABCD,且AB=AD=2,AA1=![]() ,∠BAD=120°.
,∠BAD=120°.
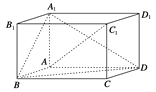
(1)求异面直线A1B与AC1所成角的余弦值;
(2)求二面角B-A1D-A的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥PABCD中,AB∥CD ,且∠BAP=∠CDP =90°.

(1).证明:平面PAB⊥平面PAD;
(2).若PA=PD=AB=DC, ∠APD =90°,且四棱锥PABCD的体积为![]() ,求该四棱锥的侧面积.
,求该四棱锥的侧面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)
已知抛物线C的方程C:y2="2" p x(p>0)过点A(1,-2).
(I)求抛物线C的方程,并求其准线方程;
(II)是否存在平行于OA(O为坐标原点)的直线l,使得直线l与抛物线C有公共点,且直线OA与l的距离等于![]() ?若存在,求出直线l的方程;若不存在,说明理由。
?若存在,求出直线l的方程;若不存在,说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() ,
,![]() ,则下列结论正确的是( )
,则下列结论正确的是( )
A. 把![]() 上所有的点向右平移
上所有的点向右平移![]() 个单位长度,再把所有图象上各点的横坐标缩短到原来的
个单位长度,再把所有图象上各点的横坐标缩短到原来的![]() 倍(纵坐标不变),得到曲线
倍(纵坐标不变),得到曲线![]()
B. 把![]() 上所有点向左平移
上所有点向左平移![]() 个单位长度,再把所得图象上各点的横坐标伸长到原来的3倍(纵坐标不变),得到曲线
个单位长度,再把所得图象上各点的横坐标伸长到原来的3倍(纵坐标不变),得到曲线![]()
C. 把![]() 上各点的横坐标缩短到原来的
上各点的横坐标缩短到原来的![]() 倍(纵坐标不变),再把所得图象上所有的点向左平移
倍(纵坐标不变),再把所得图象上所有的点向左平移![]() 个单位长度,得到曲线
个单位长度,得到曲线![]()
D. 把![]() 上各点的横坐标伸长到原来的3倍(纵坐标不变),再把所得图象上所有的点向左平移
上各点的横坐标伸长到原来的3倍(纵坐标不变),再把所得图象上所有的点向左平移![]() 个单位长度,得到曲线
个单位长度,得到曲线![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com