
科目:高中数学 来源: 题型:解答题
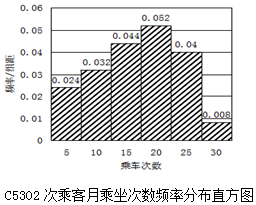 孝汉城铁于12月1日开通,C5302、C5321两列车乘务组工作人员为了了解乘坐本次列车的乘客每月需求情况,分别在两个车次各随机抽取了100名旅客进行调查,下面是根据调查结果,绘制了乘车次数的频率分布直方图和频数分布表.
孝汉城铁于12月1日开通,C5302、C5321两列车乘务组工作人员为了了解乘坐本次列车的乘客每月需求情况,分别在两个车次各随机抽取了100名旅客进行调查,下面是根据调查结果,绘制了乘车次数的频率分布直方图和频数分布表.| 乘车次数分组 | 频数 |
| [0,5) | 15 |
| [5,10) | 20 |
| [10,15) | 25 |
| [15,20) | 24 |
| [20,25) | 11 |
| [25,30] | 5 |
| 老乘客 | 新乘客 | 合计 | |
| 50岁以上 | 10 | 25 | 35 |
| 50岁以下 | 30 | 35 | 65 |
| 合计 | 40 | 60 | 100 |
| P(k2≥k0) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| k0 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{5}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,1] | B. | (-1,1] | C. | (-1,+∞) | D. | (-∞,-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,△ABC中,AB=BC,∠ABC=120°,若以A,B为焦点的双曲线的渐近线经过点C,则该双曲线的离心率为( )
如图,△ABC中,AB=BC,∠ABC=120°,若以A,B为焦点的双曲线的渐近线经过点C,则该双曲线的离心率为( )| A. | $\frac{2\sqrt{3}}{3}$ | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{5}}{2}$ | D. | $\frac{\sqrt{7}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {4,5} | B. | {2,3} | C. | {1} | D. | {4} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
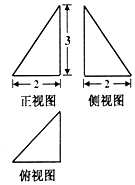 已知某三棱锥的三视图(单位:cm)如图所示,则此三棱锥的体积是2cm3,表面积是5+3$\sqrt{2}$+$\sqrt{13}$cm2.
已知某三棱锥的三视图(单位:cm)如图所示,则此三棱锥的体积是2cm3,表面积是5+3$\sqrt{2}$+$\sqrt{13}$cm2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com