练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】(2015·四川）如图，A ， B ， C ， D为平面四边形ABCD的四个内角.

    （1）证明：tan=
    （2）若A+C=180°， AB=6， BC=3， CD=4， AD=5， 求tan+tan+tan+tan的值.

    【答案】
    （1）

    见解析。


    （2）


    【解析】（1）tan===.
    (2)由A+C=180°， 得C=180°-A， D=180°-B，由（1）， 有tan+tan+tan+tan=+++=连接BD， 在△ABD中，有BD2=AB2+AD2-2AB·ADcosA. 在△ABD中，有BD2=BC2+CD2-2BC·CDcosC.
    所以AB2+AD2-2AB·ADcosA=BC2+CD2+2BC·CDcosA. 则cosA===.
    于是sinA===,连接AC， 同理可得cosB===， 于是sinB===, 所以tan+tan+tan+tan==+=.
    【考点精析】本题主要考查了余弦定理的定义的相关知识点，需要掌握余弦定理:;;才能正确解答此题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知椭圆C： 的左右焦点与其短轴的一个端点是正三角形的三个顶点，点D 在椭圆C上，直线l：y=kx+m与椭圆C相交于A、P两点，与x轴、y轴分别相交于点N和M，且PM=MN，点Q是点P关于x轴的对称点，QM的延长线交椭圆于点B，过点A、B分别作x轴的垂涎，垂足分别为A1、B1
    （1）求椭圆C的方程；
    （2）是否存在直线l，使得点N平分线段A1B1？若存在，求求出直线l的方程，若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】(2015·新课标I卷）在直角坐标系xoy中，曲线C：y=与直线y=kx+a(a＞0)交与M,N两点，
    （1）当k=0时，分别求C在点M和N处的切线方程；
    （2）y轴上是否存在点P ， 使得当k变动时，总有∠OPM=∠OPN？说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】(2015·四川）一辆小客车上有5个座位，其座位号为1，2，3，4，5，乘客P1 ， P2 ， P3 ， P4 ， P5的座位号分别为1，2，3，4，5，他们按照座位号顺序先后上车，乘客P1因身体原因没有坐自己号座位，这时司机要求余下的乘客按以下规则就坐：如果自己的座位空着，就只能坐自己的座位.如果自己的座位已有乘客就坐，就在这5个座位的剩余空位中选择座位.
    （1）（I)若乘客P1坐到了3号座位，其他乘客按规则就座，则此时共有4种坐法.下表给出其中两种坐法，请填入余下两种坐法(将乘客就坐的座位号填入表中空格处)　　

    乘客

    P1

    P2

    P3

    P4

    P5

    座位号

    3

    2

    1

    4

    5

    3

    2

    4

    5

    1


    （2）(Ⅱ)若乘客P1坐到了2号座位，其他乘客按规则就坐，求乘客P1坐到5号座位的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】(2015·四川）如图，四边形ABCD和ADPQ均为正方形，它们所在的平面互相垂直，动点M在线段PQ上，E、F分别为AB、BC的中点。设异面直线EM与AF所成的角为，则cos的最大值为 .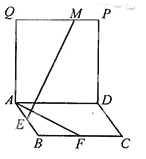

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】(2015·陕西）如图1，在直角梯形ABCD中，AD∥BC，BAD=，AB=BC=1，
    AD=2， E是AD的中点，0是AC与BE的交点．将△ABE沿BE折起到△A1BE的位置，如图2．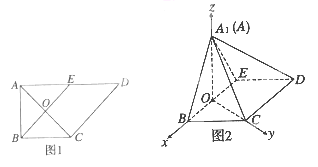

    （1）证明：CD⊥平面A1OC
    （2）若平面A1BE⊥平面BCDE， 四棱锥A1-BCDE的体积为36，求a的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】(2015·陕西）“sin=cos”是“cos2=0”的（ ）
    A.充分不必要条件
    B.必要不充分条件
    C.充分必要条件
    D.既不充分也不必要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】(2015·湖南）如图，直三棱柱ABC-A1B1C1的底面是边长为2的正三角形，E,F分别是BC,CC1的中点。

    （1）证明：平面AEF⊥平面B1BCC1；
    （2）若直线AC1与平面AA1BB1所成的角为45°，求三棱锥F-AEC的体积。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某企业为了解下属某部门对本企业职工的服务情况，随机访问50名职工，根据这50名职工对该部门的评分，绘制频率分布直方图（如图所示），其中样本数据分组区间为
    （Ⅰ）求频率分布图中a的值；
    （Ⅱ）估计该企业的职工对该部门评分不低于80的概率；
    （Ⅲ）从评分在的受访职工中，随机抽取2人，求此2人评分都在的概率。

    查看答案和解析>>

    同步练习册答案