
【题目】已知直线![]() 与
与![]() 轴相交于点
轴相交于点![]() ,点
,点![]() 坐标为
坐标为![]() ,过点
,过点![]() 作直线
作直线![]() 的垂线,交直线
的垂线,交直线![]() 于点
于点![]() .记过
.记过![]() 、
、![]() 、
、![]() 三点的圆为圆
三点的圆为圆![]() .
.
(1)求圆![]() 的方程;
的方程;
(2)求过点![]() 与圆
与圆![]() 相交所得弦长为
相交所得弦长为![]() 的直线方程.
的直线方程.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() .
.
【解析】
(1)根据题意,由直线![]() 的方程求出
的方程求出![]() 的坐标,分析可得圆
的坐标,分析可得圆![]() 是以
是以![]() 为直径的圆,求出圆心与半径,结合圆的标准方程分析可得答案;
为直径的圆,求出圆心与半径,结合圆的标准方程分析可得答案;
(2)根据题意,设要求直线为![]() ,计算出圆心
,计算出圆心![]() 到直线
到直线![]() 的距离为
的距离为![]() ,分两种情况讨论:①直线
,分两种情况讨论:①直线![]() 的斜率存在,可得出直线
的斜率存在,可得出直线![]() 的方程为
的方程为![]() ,验证即可;②当直线
,验证即可;②当直线![]() 的斜率存在时,设直线
的斜率存在时,设直线![]() 的方程为
的方程为![]() ,利用圆心到直线
,利用圆心到直线![]() 的距离求出
的距离求出![]() 的值.综合可得出所求直线的方程.
的值.综合可得出所求直线的方程.
(1)根据题意,直线![]() 与
与![]() 轴相交于点
轴相交于点![]() ,则
,则![]() ,
,
又由![]() ,则
,则![]() ,
,
则圆![]() 是以
是以![]() 为直径的圆,其圆心
为直径的圆,其圆心![]() ,半径
,半径![]() ,
,
因此,圆![]() 的方程为
的方程为![]() ;
;
(2)直线![]() 的方程为
的方程为![]() ,联立
,联立![]() ,解得
,解得![]() ,即点
,即点![]() .
.
设要求直线为![]() ,且与圆
,且与圆![]() 的交点为
的交点为![]() 、
、![]() ,
,
圆心到直线![]() 的距离
的距离![]() ,
,
分两种情况讨论:
①当直线![]() 的斜率不存在,则
的斜率不存在,则![]() 的方程为
的方程为![]() ,
,
易得圆心![]() 到直线
到直线![]() 的距离为
的距离为![]() ,符合题意;
,符合题意;
②当直线![]() 的斜率不存在,设直线
的斜率不存在,设直线![]() 的方程为
的方程为![]() ,即
,即![]() ,
,
若圆心![]() 到直线
到直线![]() 的距离为
的距离为![]() ,则有
,则有![]() ,解得
,解得![]() ,
,
则此时直线![]() 的方程为
的方程为![]() .
.
综上所述,所求直线的方程为![]() 或
或![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】在直角梯形PBCD中,∠D=∠C![]() ,BC=CD=2,PD=4,A为PD的中点,如图1,将△PAB沿AB折到△SAB的位置,使SB⊥BC,点E在SD上,如图2.
,BC=CD=2,PD=4,A为PD的中点,如图1,将△PAB沿AB折到△SAB的位置,使SB⊥BC,点E在SD上,如图2.
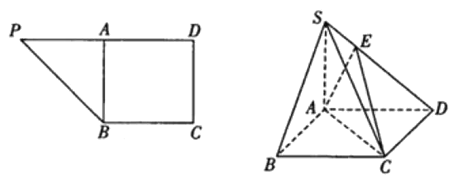
(1)求证:SA⊥平面ABCD;
(2)若E为SD中点,求D点到面EAC的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,椭圆
中,椭圆![]() 的离心率
的离心率![]() ,且点
,且点![]() 在椭圆
在椭圆![]() 上.
上.
(1)求椭圆![]() 的方程;
的方程;
(2)若点![]() 都在椭圆
都在椭圆![]() 上,且
上,且![]() 中点
中点![]() 在线段
在线段![]() (不包括端点)上.
(不包括端点)上.
①求直线![]() 的斜率;
的斜率;
②求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方形![]() 与梯形
与梯形![]() 所在的平面互相垂直,
所在的平面互相垂直, ![]() ,
,![]() ,点
,点![]() 在线段
在线段![]() 上.
上.
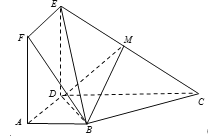
(Ⅰ) 若点![]() 为
为![]() 的中点,求证:
的中点,求证:![]() 平面
平面![]() ;
;
(Ⅱ) 求证:平面![]() 平面
平面![]() ;
;
(Ⅲ) 当平面![]() 与平面
与平面![]() 所成二面角的余弦值为
所成二面角的余弦值为![]() 时,求
时,求![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,若椭圆经过点
,若椭圆经过点![]() ,且
,且![]() 的面积为
的面积为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设斜率为![]() 的直线
的直线![]() 与以原点为圆心,半径为
与以原点为圆心,半径为![]() 的圆交于
的圆交于![]() ,
,![]() 两点,与椭圆
两点,与椭圆![]() 交于
交于![]() ,
,![]() 两点,且
两点,且![]() ,当
,当![]() 取得最小值时,求直线
取得最小值时,求直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com