
| A. | $\frac{1}{2}$ | B. | $\frac{3}{4}$ | C. | $\frac{1}{6}$ | D. | 0 |
分析 写出所有基本事件(a,b)的取法,求出满足f(x)在区间(-∞,-1]上是减函数的(a,b)的个数,然后利用古典概型概率计算公式求得概率;
解答 解:函数f(x)=$\frac{1}{2}$ax2+bx+1,其中a∈{2,4},b∈{1,3},
从f(x)中随机抽取1个,
基本事件总数n=2×2=4,
即f(x)共有四种等可能基本事件,分别为(a,b)取(2,1)(2,3)(4,1)(4,3),
记事件A为“f(x)在区间(-∞,-1]上是减函数”,
由条件知f(x)开口一定向上,对称轴为x=-$\frac{b}{a}$,
事件A共有三种(2,1)(4,1)(4,3)等可能基本事件,
则P(A)=$\frac{3}{4}$.
∴f(x)在区间(-∞,-1]上是减函数的概率为$\frac{3}{4}$.
故选:B.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意列举法的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}{e^3}$ | B. | $\frac{{\sqrt{2}}}{2}{e^3}$ | C. | $\frac{{\sqrt{3}}}{2}{e^3}$ | D. | e3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
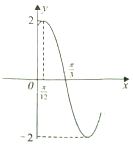 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,把f(x)的图象向右平移$\frac{π}{3}$个单位长度得到g(x)的图象,则g(x)的单调递增区间是( )
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,把f(x)的图象向右平移$\frac{π}{3}$个单位长度得到g(x)的图象,则g(x)的单调递增区间是( )| A. | $[{kπ-\frac{5π}{12},kπ+\frac{π}{12}}],k∈z$ | B. | $[{kπ-\frac{π}{6},kπ+\frac{π}{3}}],k∈z$ | ||
| C. | $[{kπ-\frac{π}{12},kπ+\frac{5π}{12}}],k∈z$ | D. | $[{kπ+\frac{π}{6},kπ+\frac{5π}{6}}],k∈z$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{2}$ | D. | $\frac{3π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2015-2016学年江西省南昌市高二理下学期期末考试数学试卷(解析版) 题型:选择题
设函数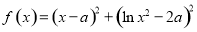 ,其中
,其中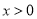 ,
,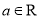 ,存在
,存在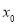 使得
使得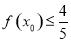 成立,则实数
成立,则实数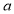 的值为( )
的值为( )
A. B.
B.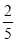 C.
C.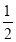 D.
D.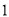
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com