
已知函数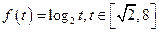 .
.
(1)求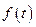 的值域G;
的值域G;
(2)若对于G内的所有实数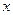 ,不等式
,不等式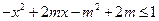 恒成立,求实数
恒成立,求实数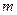 的取值范围.
的取值范围.
解:(Ⅰ)∵f(t)=log2t在t∈[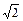 ,8]上是单调递增的,∴log2
,8]上是单调递增的,∴log2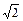 ≤log2t≤log28.
≤log2t≤log28.
即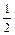 ≤f(t)≤3.∴f(t)的值域G为[
≤f(t)≤3.∴f(t)的值域G为[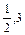 ]. -------4 分
]. -------4 分
(Ⅱ)由题知-x2+2mx-m2+2m≤1在x∈[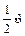 ]上恒成立
]上恒成立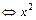 -2mx+m2-2m+1≥0在x∈[
-2mx+m2-2m+1≥0在x∈[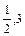 ]上恒成
]上恒成 立.-----6分
立.-----6分
令g(x)=x2-2mx+m2-2m+1,x∈[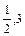 ].只需gmin(x)≥0即可.
].只需gmin(x)≥0即可.
而g(x)=(x-m)2-2m+1,x∈[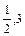 ].
].
(1)当 m≤
m≤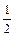 时,gmin(x)=g(
时,gmin(x)=g(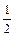 )=
)=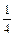 -3m+m2+1≥0.∴4m2-12m+5≥0.解得m≥
-3m+m2+1≥0.∴4m2-12m+5≥0.解得m≥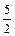 或m≤
或m≤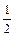
.∴m≤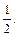
(2)当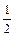 <m<3时,gmin(x)=g(m)= -2m+1≥0.解得m≤
<m<3时,gmin(x)=g(m)= -2m+1≥0.解得m≤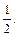 这与
这与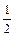 <m<3矛盾.----10
<m<3矛盾.----10
(3)当m≥3时,gmin(x)=g(3)=10 +m2-8m≥0.解得m≥4+
+m2-8m≥0.解得m≥4+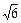 或m≤4-
或m≤4-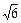 .而m≥3,
.而m≥3,
∴m≥4+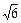 . ----12分综上,实数m的取值范围是 (-∞,
. ----12分综上,实数m的取值范围是 (-∞,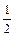 )∪[4+
)∪[4+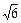 ,+∞].
,+∞].
解析


科目:高中数学 来源: 题型:解答题
某公司生产陶瓷,根据历年的情况可知,生产陶瓷每天的固定成本为14000元,每生产一件产品,成本增加210元.已知该产品的日销售量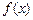 与产量
与产量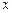 之间的关系式为
之间的关系式为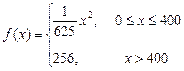 ,每件产品的售价
,每件产品的售价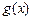 与产量
与产量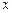 之间的关系式为
之间的关系式为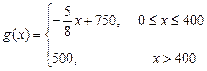 .
.
(Ⅰ)写出该陶瓷厂的日销售利润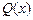 与产量
与产量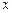 之间的关系式;
之间的关系式;
(Ⅱ)若要使得日销售利润最大,每天该生产多少件产品,并求出最大利润.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数f (x)=lg(ax-bx)(a >1,0< b<1)
(1) 求f (x) 的定义域;
的定义域;
(2) 此函数的图象上是否存在两点,过这两点的直线平行于x轴?
(3) 当a、b满足什么条件时f (x)恰在(1,+∞)取正值
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
.(12分)已知函数 的定义域为
的定义域为 ,且同时满足:(Ⅰ)对任意
,且同时满足:(Ⅰ)对任意 ,总有
,总有 ;(Ⅱ)
;(Ⅱ)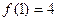 ;(Ⅲ)若
;(Ⅲ)若 ,则有
,则有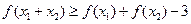
(1)试求 的值;
的值;
(2)试求函数 的最大值;
的最大值;
(3)试证明:当 时,
时, 。
。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
已知p:方程x2+mx+1=0有两个不等的 负实根,q:方程4x2+4(m-2)x+1=0无实根。若p或q为真,p且q为假。求实数m的取值范围。
负实根,q:方程4x2+4(m-2)x+1=0无实根。若p或q为真,p且q为假。求实数m的取值范围。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com