
【题目】对于定义域为![]() 的函数
的函数![]() ,若满足①
,若满足①![]() ;②当
;②当![]() ,且
,且![]() 时,都有
时,都有![]() ;③当
;③当![]() ,且
,且![]() 时,
时, ![]() ,则称
,则称![]() 为“偏对称函数”.现给出四个函数:
为“偏对称函数”.现给出四个函数:
①![]() ; ②
; ② 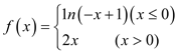 ;
;
③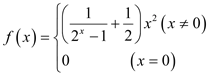 ; ④
; ④![]() .
.
则其中是“偏对称函数”的函数为__________.
【答案】②④
【解析】由当![]() ,且
,且![]() 时,都有
时,都有![]() 可得
可得![]() 或
或![]() ,即条件②等价于函数
,即条件②等价于函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增
上单调递增
对于![]() ,显然满足①,且易证
,显然满足①,且易证![]() 是偶函数,当
是偶函数,当![]() 时,
时, ![]() ,所以
,所以![]() 在
在![]() 上单调递增,因为
上单调递增,因为![]() 是偶函数,所以
是偶函数,所以![]() 在
在![]() 上单调递减,满足条件②,由
上单调递减,满足条件②,由![]() 是偶函数可得当
是偶函数可得当![]() ,且
,且![]() 时,
时, ![]() ,故不满足条件③;
,故不满足条件③;
对于![]() ,显然满足条件①,当
,显然满足条件①,当![]() 时,
时, ![]() ,则
,则![]() 在
在![]() 上单调递增,当
上单调递增,当![]() 时,
时, ![]() ,由复合函数单调性法则可知
,由复合函数单调性法则可知![]() 在
在![]() 上单调递减,故满足条件②,由函数的单调性可知,当
上单调递减,故满足条件②,由函数的单调性可知,当![]() 时,且
时,且![]() 时,
时, ![]() ,不妨设
,不妨设![]() ,则
,则![]() ,设
,设![]() ,则
,则![]() ,
, ![]() 在
在![]() 上单调递减,所以
上单调递减,所以![]() ,即
,即![]() ,即
,即![]() ,所以
,所以![]() ,即
,即![]() 满足条件③;
满足条件③;
对于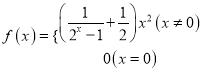 ,易证
,易证![]() 是奇函数,由奇函数的性质可得,
是奇函数,由奇函数的性质可得, ![]() 在
在![]() 和
和![]() 上的单调性相同,故不满足②;
上的单调性相同,故不满足②;
对于![]() ,显然满足条件①,
,显然满足条件①,![]() ,则
,则![]() ,满足条件②,由
,满足条件②,由![]() 的单调性知当
的单调性知当![]() 时,且
时,且![]() 时,
时, ![]() ,不妨设
,不妨设![]() ,则
,则![]() ,
, ![]() ,
, ![]()
令![]() ,则
,则![]() ,当且仅当
,当且仅当![]() 即
即![]() 时,取等号,所以
时,取等号,所以![]() 在
在![]() 上是增函数,所以
上是增函数,所以![]() ,即
,即![]() ,所以
,所以![]() ,即
,即![]() ,所以
,所以![]() ,满足条件③;
,满足条件③;
故答案为②④


科目:高中数学 来源: 题型:
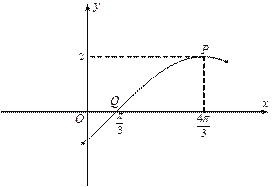
【题目】如图为函数![]() 图像的一部分,其中点
图像的一部分,其中点![]() 是图像的一个最高点,点
是图像的一个最高点,点![]() 是与点
是与点![]() 相邻的图像与
相邻的图像与![]() 轴的一个交点.
轴的一个交点.
⑴ 求函数![]() 的解析式;
的解析式;
⑵ 若将函数![]() 的图像沿
的图像沿![]() 轴向右平移
轴向右平移![]() 个单位,再把所得图像上每一点的横坐标都变为原来的
个单位,再把所得图像上每一点的横坐标都变为原来的![]() (纵坐标不变),得到函数
(纵坐标不变),得到函数![]() 的图像,求函数
的图像,求函数![]() 的单调递增区间.
的单调递增区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2013年第三季度,国家电网决定对城镇居民用电计费标准作出调整,并根据用电情况将居民分为三类:第一类的用电区间在(0,170],第二类在(170,260],第三类在(260,+∞)(单位:千瓦时).某小区共有1000户居民,现对他们的用电情况进行调查,得到频率分布直方图,如图所示.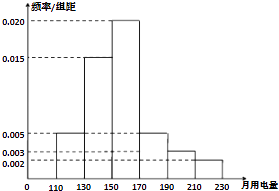
(1)求该小区居民用电量的中位数与平均数;
(2)本月份该小区没有第三类的用电户出现,为鼓励居民节约用电,供电部门决定:对第一类每户奖励20元钱,第二类每户奖励5元钱,求每户居民获得奖励的平均值;
(3)利用分层抽样的方法从该小区内选出5位居民代表,若从该5户居民代表中任选两户居民,求这两户居民用电资费属于不同类型的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高三年级在高校自主招生期间,把学生的平时成绩按“百分制”折算并排序,选出前300名学生,并对这300名学生按成绩分组,第一组[75,80),第二组[80,85),第三组[85,90),第四组[90,95),第五组[95,100],如图为频率分布直方图的一部分,其中第五组、第一组、第四组、第二组、第三组的人数依次成等差数列. (Ⅰ)请在图中补全频率分布直方图;
(Ⅱ)若B大学决定在成绩高的第4,5组中用
分层抽样的方法抽取6名学生,并且分成2组,每组3人
进行面试,求95分(包括95分)以上的同学被分在同一个小组的概率.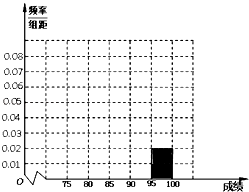
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某理科考生参加自主招生面试,从7道题中(4道理科题3道文科题)不放回地依次任取3道作答.
(1)求该考生在第一次抽到理科题的条件下,第二次和第三次均抽到文科题的概率;
(2)规定理科考生需作答两道理科题和一道文科题,该考生答对理科题的概率均为![]() ,答对文科题的概率均为
,答对文科题的概率均为![]() ,若每题答对得10分,否则得零分.现该生已抽到三道题(两理一文),求其所得总分
,若每题答对得10分,否则得零分.现该生已抽到三道题(两理一文),求其所得总分![]() 的分布列与数学期望
的分布列与数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校某研究性学习小组在对学生上课注意力集中情况的调查研究中,发现其在40分钟的一节课中,注意力指数y与听课时间x(单位:分钟)之间的关系满足如图所示的图象,当x∈(0,12]时,图象是二次函数图象的一部分,其中顶点A(10,80),过点B(12,78);当x∈[12,40]时,图象是线段BC,其中C(40,50).根据专家研究,当注意力指数大于62时,学习效果最佳. 
(1)试求y=f(x)的函数关系式;
(2)教师在什么时段内安排内核心内容,能使得学生学习效果最佳?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知长方体ABCD﹣A'B'C'D'中,AB=4,AD=3,AA'=2; 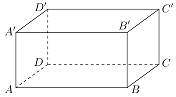
(1)求出异面直线AC'和BD所成角的余弦值;
(2)找出AC'与平面D'DBB'的交点,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com