【题目】关于x的不等式ax2+bx+c＜0的解集为{x|x＜﹣2或x＞﹣ 
}，则关于x的不等式ax2﹣bx+c＞0的解集为 ．
【答案】
【解析】解：∵关于x的不等式ax2+bx+c＜0的解集为{x|x＜﹣2或x＞﹣ 
}， ∴a＜0，且方程ax2+bx+c=0的根为x=﹣2或x=﹣ ，
由根与系数的关系式得：
﹣2+（﹣ ）=﹣ 
，（﹣2）×（﹣ ）= 
，
即 = 
， =1；
又关于x的不等式ax2﹣bx+c＞0可化为
x2﹣ x+ ＜0，
即x2﹣ x+1＜0，
解不等式，得 ＜x＜2，
∴不等式ax2﹣bx+c＞0的解集为{x| ＜x＜2}；
所以答案是：{x| ＜x＜2}．
【考点精析】根据题目的已知条件，利用解一元二次不等式的相关知识可以得到问题的答案，需要掌握求一元二次不等式
解集的步骤：一化：化二次项前的系数为正数;二判：判断对应方程的根;三求：求对应方程的根;四画：画出对应函数的图象;五解集：根据图象写出不等式的解集;规律：当二次项系数为正时，小于取中间，大于取两边．
红果子三级测试卷系列答案
课堂练加测系列答案科目：高中数学 来源： 题型：
【题目】现有1名女教师和2名男教师参加说题比赛，共有2道备选题目，若每位选手从中有放回地随机选出一道题进行说题，其中恰有一男一女抽到同一道题的概率为（ ）
A.
B.
C.
D.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知一组数据x1 ， x2 ， x3 ， x4 ， x5的平均数是2，方差是 
，那么另一组数据2x1﹣1，2x2﹣1，2x3﹣1，2x4﹣1，2x5﹣1的平均数，方差分别是（ ）
A.3， 
B.3， 
C.4，
D.4，
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知 
=（ 
sinx，m+cosx）， 
=（cosx，﹣m+cosx），且f（x）= 
（1）求函数f（x）的解析式；
（2）当x∈ 
时，f（x）的最小值是﹣4，求此时函数f（x）的最大值，并求出相应的x的值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】为了了解甲、乙两个工厂生产的轮胎的宽度是否达标，分别从两厂随机各选取了10个轮胎，将每个轮胎的宽度（单位：mm）记录下来并绘制出如下的折线图：
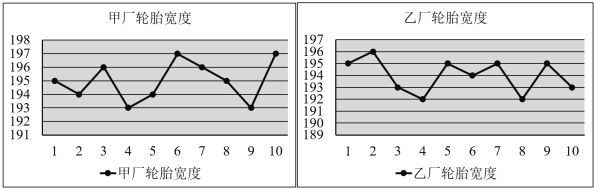
（1）分别计算甲、乙两厂提供的10个轮胎宽度的平均值；
（2）轮胎的宽度在
内，则称这个轮胎是标准轮胎.试比较甲、乙两厂分别提供的10个轮胎中所有标准轮胎宽度的方差的大小，根据两厂的标准轮胎宽度的平均水平及其波动情况，判断这两个工厂哪个厂的轮胎相对更好？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】原命题：“
， 
为两个实数，若
，则
， 
中至少有一个不小于1”，下列说法错误的是（ ）
A. 逆命题为：若
， 
中至少有一个不小于1，则
，为假命题
B. 否命题为：若
，则
， 
都小于1，为假命题
C. 逆否命题为：若
， 
都小于1，则
，为真命题
D. “
”是“
， 
中至少有一个不小于1”的必要不充分条件
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设数列{an}的前n项和为Sn ， 设an是Sn与2的等差中项，数列{bn}中，b1=1，点P（bn ， bn+1）在直线y=x+2上．
（1）求an ， bn；
（2）若数列{bn}的前n项和为Bn ， 比较 
+ 
+…+ 
与1的大小．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
