
【题目】微信是现代生活中进行信息交流的重要工具.据统计,某公司200名员工中![]() 的人使用微信,其中每天使用微信时间少于一小时的有60人,其余的员工每天使用微信时间不少于一小时,若将员工分成青年(年龄小于40岁)和中年(年龄不小于40岁)两个阶段,那么使用微信的人中
的人使用微信,其中每天使用微信时间少于一小时的有60人,其余的员工每天使用微信时间不少于一小时,若将员工分成青年(年龄小于40岁)和中年(年龄不小于40岁)两个阶段,那么使用微信的人中![]() 是青年人.若规定:每天使用微信时间不少于一小时为经常使用微信,那么经常使用微信的员工中
是青年人.若规定:每天使用微信时间不少于一小时为经常使用微信,那么经常使用微信的员工中![]() 都是青年人.
都是青年人.
(1)若要调查该公司使用微信的员工经常使用微信与年龄的关系,完成![]() 列联表:
列联表:
青年人 | 中年人 | 合计 | |
经常使用微信 | |||
不经常使用微信 | |||
合计 |
(2)由列联表中所得数据判断,能否在犯错误的概率不超过![]() 的前提下认为“经常使用微信与年龄有关”?
的前提下认为“经常使用微信与年龄有关”?
| 0.010 | 0.001 |
| 6.635 | 10.828 |
![]()
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:高中数学 来源: 题型:
【题目】某科研小组研究发现:一棵水蜜桃树的产量![]() (单位:百千克)与肥料费用
(单位:百千克)与肥料费用![]() (单位:百元)满足如下关系:
(单位:百元)满足如下关系:![]() ,且投入的肥料费用不超过5百元.此外,还需要投入其他成本(如施肥的人工费等)
,且投入的肥料费用不超过5百元.此外,还需要投入其他成本(如施肥的人工费等)![]() 百元.已知这种水蜜桃的市场售价为16元/千克(即16百元/百千克),且市场需求始终供不应求.记该棵水蜜桃树获得的利润为
百元.已知这种水蜜桃的市场售价为16元/千克(即16百元/百千克),且市场需求始终供不应求.记该棵水蜜桃树获得的利润为![]() (单位:百元).
(单位:百元).
(1)求利润函数![]() 的函数关系式,并写出定义域;
的函数关系式,并写出定义域;
(2)当投入的肥料费用为多少时,该水蜜桃树获得的利润最大?最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的各项排成如图所示的三角形数阵,数阵中每一行的第一个数
的各项排成如图所示的三角形数阵,数阵中每一行的第一个数![]() 构成等差数列
构成等差数列![]() ,
,![]() 是
是![]() 的前
的前![]() 项和,且
项和,且![]() ,
,![]() .
.
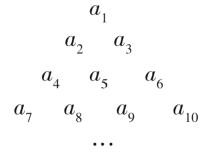
(1)若数阵中从第3行开始每行中的数按从左到右的顺序均构成公比为正数的等比数列,且公比相等,已知![]() ,求
,求![]() 的值;
的值;
(2)设![]() ,当
,当![]() 时,对任意
时,对任意![]() ,不等式
,不等式![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程,下图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况. 下列叙述中正确的是( )

A. 消耗1升汽油,乙车最多可行驶5千米
B. 以相同速度行驶相同路程,三辆车中,甲车消耗汽油最多
C. 甲车以80千米/小时的速度行驶1小时,消耗10升汽油
D. 某城市机动车最高限速80千米/小时. 相同条件下,在该市用丙车比用乙车更省油
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在平面直角坐标系中,动点P到定点F(1,0)的距离比到定直线x=-2的距离小1.
(1)求动点P的轨迹C的方程;
(2)若直线l与(1)中轨迹C交于A,B两点,通过A和原点O的直线交直线x=-1于D,求证:直线DB平行于x轴.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司设计如图所示的环状绿化景观带,该景观带的内圈由两条平行线段(图中的![]() )和两个半圆构成,设
)和两个半圆构成,设![]() ,且
,且![]() .
.
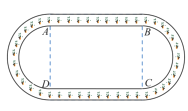
(1)若内圈周长为![]() ,则
,则![]() 取何值时,矩形
取何值时,矩形![]() 的面积最大?
的面积最大?
(2)若景观带的内圈所围成区域的面积为![]() ,则
,则![]() 取何值时,内圈周长最小?
取何值时,内圈周长最小?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列有关命题的说法正确的有( )
(1)若p∧q为假命题,则p、q均为假命题;
(2)“x=1”是“x2﹣3x+2=0”的充分不必要条件;
(3)若“p∨q”为假命题,则“¬p∧¬q”为真命题.
(4)命题“若x2﹣3x+2=0,则x=1”的逆否命题为:“若x≠1,则x2﹣3x+2≠0”
A.1个B.2个C.3个D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com