
分析 已知等式利用正弦定理化简,再根据G为三角形重心,利用中线的性质及向量法则变形,求出a,b,c,利用余弦定理表示出cosB,即可确定出B的度数.
解答 解:∵G是重心,∴$\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}$,
∴$\overrightarrow{GA}=-\overrightarrow{GB}-\overrightarrow{GC}$,
∵$\sqrt{7}\overrightarrow{GA}sinA+3\overrightarrow{GB}sinB+3\sqrt{7}\overrightarrow{GC}sinC=\overrightarrow 0$,
∴$\sqrt{7}$(-$\overrightarrow{GB}-\overrightarrow{GC}$)sinA+3$\overrightarrow{GB}$sinB+3$\sqrt{7}$$\overrightarrow{GC}$sinC=$\overrightarrow{0}$,
∴(3sinB-$\sqrt{7}$sinA)$\overrightarrow{GB}$+(3$\sqrt{7}$sinC-$\sqrt{7}$sinA)$\overrightarrow{GC}$=$\overrightarrow{0}$,
∵$\overrightarrow{GB}$,$\overrightarrow{GC}$不共线,
∴3sinB=$\sqrt{7}$sinA=3$\sqrt{7}$sinC,
∴3b=$\sqrt{7}$a=3$\sqrt{7}$c,
设3b=$\sqrt{7}$a=3$\sqrt{7}$c=k,k>0,
则a=$\frac{k}{\sqrt{7}}$,b=$\frac{k}{3}$,c=$\frac{k}{3\sqrt{7}}$,
∴cosB=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$=$\frac{\frac{{k}^{2}}{7}+\frac{{k}^{2}}{63}-\frac{{k}^{2}}{9}}{2×\frac{k}{\sqrt{7}}×\frac{k}{3\sqrt{7}}}$=$\frac{1}{2}$,
0°<B<180°
∴B=60°.
故答案为:60°.
点评 此题考查了正弦、余弦定理,以及平面向量的数量积运算,熟练掌握定理是解本题的关键.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
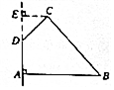 如图,在四边形ABCD中,∠DAB=90°,∠ADC=135°,AB=5,CD=2$\sqrt{2}$,AD=2,则四边形ABCD绕AD旋转一周所成几何体的表面积为( )
如图,在四边形ABCD中,∠DAB=90°,∠ADC=135°,AB=5,CD=2$\sqrt{2}$,AD=2,则四边形ABCD绕AD旋转一周所成几何体的表面积为( )| A. | (60+4$\sqrt{2}$)π | B. | (60+8$\sqrt{2}$)π | C. | (56+8$\sqrt{2}$)π | D. | (56+4$\sqrt{2}$)π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
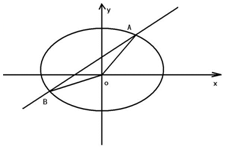 已知椭圆C的中心在坐标原点,一个焦点的坐标为$(\sqrt{3},0)$,椭圆C经过点P$(1,\frac{{\sqrt{3}}}{2})$.
已知椭圆C的中心在坐标原点,一个焦点的坐标为$(\sqrt{3},0)$,椭圆C经过点P$(1,\frac{{\sqrt{3}}}{2})$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(-n)<f(n-1)<f(n+1) | B. | f(n-1)<f(-n)<f(n+1) | C. | f(n+1)<f(-n)<f(n-1) | D. | f(n+1)<f(n-1)<f(-n) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 将某选手的9个得分去掉一个最高分,去掉一个最低分,7个剩余分数的平均分为91,现场作的9个得分的茎叶图,后来有一个数据模糊,无法辨认,在图中以x表示,则x为4.
将某选手的9个得分去掉一个最高分,去掉一个最低分,7个剩余分数的平均分为91,现场作的9个得分的茎叶图,后来有一个数据模糊,无法辨认,在图中以x表示,则x为4.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com