��ȱ�����{an}��ǰn��ĺ�ΪSn������Ϊq��q��1����
��1����S4��S12��S8�ɵȲ����У���֤��a10��a18��a14�ɵȲ����У�
��2����Sm��Sk��St��m��k��tΪ������ȵ����������ɵȲ����У���������{an}���Ƿ���ڲ�ͬ������ɵȲ����У������ڣ�д������������������ڣ���˵�����ɣ�
��3����qΪ����1��������������{an}���Ƿ����һ��ak��ʹ��akǡ�ÿ��Ա�ʾΪ����������������ĺͣ���˵�����ɣ�
���𰸡�
��������1������S
4��S
12��S
8�ɵȲ����У�q��1���ɵ�S
12=S
4+S
8������ɵ�2q
8=1+q
4����������֤��a
10��a
18��a
14�ɵȲ����У�
��2������S
m��S
k��S
t��m��k��tΪ������ȵ����������ɵȲ����У��ɵ�2S
k=S
m+S
t������ɵ�
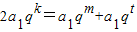
���Ӷ��ɵ�a
m+1��a
k+1��a
t+1�ɵȲ����У����ɵó����ۣ�
��3���������һ��a
k��ʹ��a
kǡ�ÿ��Ա�ʾΪ����������������ĺͣ���a
k=a
n+a
n+1���ɵ�k��n��q
k-n=1+q
���Ӷ��ɵý��ۣ�
����⣺��1����S
4��S
12��S
8�ɵȲ����У�q��1����S
12=S
4+S
8��
��
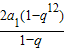
=
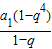
+
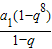
��2q
8=1+q
4��a
10+a
14=
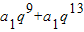
=
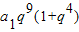
=
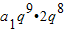
=2a
18��
��a
10��a
18��a
14�ɵȲ����У�
��2����S
m��S
k��S
t��m��k��tΪ������ȵ����������ɵȲ����У���2S
k=S
m+S
t��
��
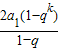
=
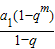
+
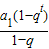
��2q
k=q
m+q
t��
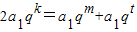
��a
m+1��a
k+1��a
t+1�ɵȲ����У�
��a
m+2��a
k+2��a
t+2�ɵȲ����У�
��3���������һ��a
k��ʹ��a
kǡ�ÿ��Ա�ʾΪ����������������ĺͣ���a
k=a
n+a
n+1��
��

��a
1��0��q��1
��q
k-1=q
n-1+q
n��q
k=q
n+q
n+1��q
n+1��1
��q
k��q
n��k��n��q
k-n=1+q
��qΪż��ʱ��q
k-nΪż������1+qΪ���������費������
��qΪ����ʱ��q
k-nΪ��������1+qΪż��������Ҳ��������
���ϣ�{a
n}�����a
k��ʹ��a
kǡ�ÿ��Ա�ʾΪ����������������ĺͣ�
���������⿼��Ȳ�������ȱ����е��ۺϣ�����Ȳ����е�֤��������ѧ�������������������������е��⣮

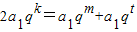 ���Ӷ��ɵ�am+1��ak+1��at+1�ɵȲ����У����ɵó����ۣ�
���Ӷ��ɵ�am+1��ak+1��at+1�ɵȲ����У����ɵó����ۣ�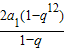 =
=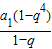 +
+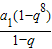
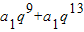 =
=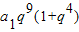 =
=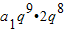 =2a18��
=2a18��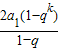 =
=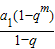 +
+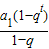
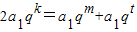



 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�