
【题目】设全集为R,集合A={x| ![]() ≥0},B={x|﹣2≤x<0},则(RA)∩B=( )
≥0},B={x|﹣2≤x<0},则(RA)∩B=( )
A.(﹣1,0)
B.[﹣1,0)
C.[﹣2,﹣1]
D.[﹣2,﹣1)
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:高中数学 来源: 题型:
【题目】甲乙两人同时生产内径为![]() 的一种零件,为了对两人的生产质量进行评比,从他们生产的零件中各抽出 5 件(单位:
的一种零件,为了对两人的生产质量进行评比,从他们生产的零件中各抽出 5 件(单位: ![]() ) ,
) ,
甲:25.44,25.43, 25.41,25.39,25.38
乙:25.41,25.42, 25.41,25.39,25.42.
从生产的零件内径的尺寸看、谁生产的零件质量较高.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为矩形,平面
为矩形,平面![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 为
为![]() 中点.
中点.

(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值;
的余弦值;
(Ⅲ)在棱![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() ?若存在,求
?若存在,求![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知一动点![]() ,
, ![]() 到点
到点![]() 的距离减去它到
的距离减去它到![]() 轴距离的差都是
轴距离的差都是![]() .
.
(![]() )求动点
)求动点![]() 的轨迹方程.
的轨迹方程.
(![]() )设动点
)设动点![]() 的轨迹为
的轨迹为![]() ,已知定点
,已知定点![]() 、
、![]() ,直线
,直线![]() 、
、![]() 与轨迹
与轨迹![]() 的另一个交点分别为
的另一个交点分别为![]() 、
、![]() .
.
(i)点![]() 能否为线段
能否为线段![]() 的中点,若能,求出直线
的中点,若能,求出直线![]() 的方程,若不能,说明理由.
的方程,若不能,说明理由.
(ii)求证:直线![]() 过定点.
过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆![]() 的左、右焦点为
的左、右焦点为![]() ,右顶点为
,右顶点为![]() ,上顶点为
,上顶点为![]() ,若
,若![]() ,
, ![]() 与
与![]() 轴垂直,且
轴垂直,且![]() .
.
(1)求椭圆方程;
(2)过点![]() 且不垂直于坐标轴的直线与椭圆交于
且不垂直于坐标轴的直线与椭圆交于![]() 两点,已知点
两点,已知点![]() ,当
,当![]() 时,求满足
时,求满足![]() 的直线
的直线![]() 的斜率
的斜率![]() 的取值范围.
的取值范围.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() 的离心率是
的离心率是![]() ,过点
,过点![]() 的动直线
的动直线![]() 与椭圆相交于
与椭圆相交于![]() 两点,当直线
两点,当直线![]() 与
与![]() 轴平行时,直线
轴平行时,直线![]() 被椭圆
被椭圆![]() 截得的线段长为
截得的线段长为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)在![]() 轴上是否存在异于点
轴上是否存在异于点![]() 的定点
的定点![]() ,使得直线
,使得直线![]() 变化时,总有
变化时,总有![]() ?若存在,求出点
?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】统计表明,家庭的月理财投入![]() (单位:千元)与月收入
(单位:千元)与月收入![]() (单位:千元)之间具有线性相关关系.某银行随机抽取5个家庭,获得第
(单位:千元)之间具有线性相关关系.某银行随机抽取5个家庭,获得第![]() (
(![]() )个家庭的月理财投入
)个家庭的月理财投入![]() 与月收入
与月收入![]() 的数据资料,经计算得
的数据资料,经计算得![]() .
.
(1)求![]() 关于
关于![]() 的回归方程
的回归方程![]() ;
;
(2)判断![]() 与
与![]() 之间是正相关还是负相关;
之间是正相关还是负相关;
(3)若某家庭月理财投入为5千元,预测该家庭的月收入.
附:回归方程的斜率与截距的最小二乘估计公式分别为:
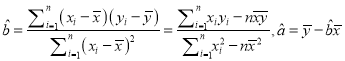 ,其中
,其中![]() 为样本平均值.
为样本平均值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知F1 , F2分别为椭圆C: ![]() +
+ ![]() =1(a>b>0)的左、右两个焦点,椭圆上点M(
=1(a>b>0)的左、右两个焦点,椭圆上点M( ![]() ,
, ![]() )到F1、F2两点的距离之和等于4.
)到F1、F2两点的距离之和等于4.
(1)求椭圆C的方程;
(2)已知过右焦点且垂直于x轴的直线与椭圆交于点N(点N在第一象限),E,F是椭圆C上的两个动点,如果kEN+KFN=0,证明直线EF的斜率为定值,并求出这个定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com